二分专题训练

机器人跳跃问题

今日头条2019，笔试题

虽然二分算法的时间复杂度为 O( logn )，由于它的常数比较小，所以它的效率非常高

当数据范围等于 10^6 的时候，在理论上二分比时间复杂度为 O( 1 ) 的哈希表运行效率慢 20 倍

题目给出了塔的高度，一共有 n + 1 座塔，n 等于 5 有 6 座塔

一开始机器人处于 0 号塔的位置，规定 0 号塔的高度一定是 0，每次机器人会从当前这个塔向后跳一个单位，后面这些塔的高度在 1 - 10^5 之间

跳的时候有一个能量值的概念，假设跳之前的能量值是 E，当前机器人处于第 k 座塔，下一次会跳到第 k + 1 座塔，假设第

k + 1 座塔的高度是 hk+1，机器人跳过去之后有一个能量的变化

从低往高跳会损失一些能量，从高往低跳，重力势能转化为动能，会增加一些能量

每跳一次，能量就会变成 2E - hk+1

题目要求从 0 号塔跳到第 n 号塔，要保证在跳的过程中，E 永远 ≥ 0，在这个限制条件下，问机器人的初始能量值最小是多少？

只考虑整数，不考虑实数和小数，其实是一个整数二分，不是实数二分

模拟样例

样例 1 为什么最小是 4？一开始能量为 4，跳到第一个位置的时候，能量由 4 变成 2 × 4 - 3 = 5，跳到第二个位置，能量由 5 变成 2 × 5 - 4 = 6，可以发现这个过程当中不会有任何情况使它的能量值小于 0 的，因此 4 是成立的，但是我们发现，如果初始能量是 4 的话，最终的能量值非常高，那么我们能不能把初始能量值降低一些呢？

接下来把初始能量值换成 3 试一下，可以发现到 5 的位置会导致能量值小于 0，不满足题目要求，因此最小初始能量值就是 4

求最小或者求最大的问题，一般来看是不是能用二分来做，就是看这个题目是不是具有二段性，在大多数情况下，二分的题目不仅具有二段性且具有单调性，如果一个题目具有单调性一定可以用二分来做，如果一个题目不具有单调性也可以用二分来做

所以先看这道题目是不是具有单调性？

如果初始能量 E0 可以满足要求，那么我们取一个大于 E0 的值 ( E' ≥ E0 ) 是否一定满足要求？

只要 E0 成立，所有 ≥ E0 的值也一定成立，这样就一定具有单调性

只要 E0 成立，意味着所有 ≥ E0 的值也一定成立，因此 E0 一定是一个最小的值，然后我们就可以把它二分出来

假设 E0 是初始值，E1 是跳到第一个塔之后的能量，E2 是跳到第二个塔之后的能量 . . . 如果 E0 成立，必然有每一个 Ei 都是大于等于 0，只要 E0 是成立的，所有大于等于 E0 的也一定成立

二分的性质，下图给出答案可能的区间，如果 E0 是答案的话，后面这一段都是满足的，前面这一段都是不满足的

 

①可以发现这道题目是具有一个二段性的性质，性质就是某一个 E 是否可以满足条件，初始值如果是这个能量的话，中间的过程是不是一定都是大于等于 0，用这个判断条件判断，一定可以把答案二分出来

②想一下二分的形式是 L 等于 mid 还是 R 等于 mid

如果 mid 可以满足要求，所有大于等于 mid 的位置也一定可以满足要求，要找一个最小的满足要求的值，因此最小的值应该在左边，而且 mid 也有可能是答案，所以我们在更新的区间的时候应该是把 R 更新成 mid，否则如果 mid 不满足要求，意味着所有小于等于 mid 的部分都是不满足要求的，而且 mid 本身也是不满足要求的，因此答案一定在 mid + 1 以及后面的部分

怎么实现 check 函数，怎么判断每一项是不是大于等于 0？

每一项都可以用前面一项推导出来，所以我们只需要递推一遍，判断中间有没有 0 就可以了，如果递推的过程当中没有出现 0 的话，那么它就是成立的，返回 true，否则返回 false

check 函数直接递推一遍就可以了，可以发现每一次更新的时候，后一个 E 都等于前一个 E 的两倍减去一个值，如果 h 取一个很小的值，大致上每一个 Ei = 2Ei - 1，很可能会爆 int，因为它每次乘 2

怎么处理爆 int 的情况？中间值达到什么程度就一定是成功的呢？

假设所有建筑物高度的最大值是 maxh，如果 E 在某一个时刻等于 maxh，E 在更新的时候为 2E - hi，只要在中间的时刻，

E ≥ maxh，maxh 是所有 hi 的最大值，maxh 大于 hi ，所以 maxh - hi 这一项必然是大于 0 的，如果在中间时刻，E 大于等于 maxh，就意味着这个 E 一定是严格递增的，不可能递减，后面所有 E 都是大于等于 0 的，直接返回 true，防止中间过程爆 int

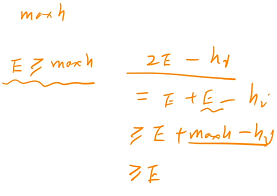
怎么求 maxh？

maxh 是所有高度的最大值，在读入的时候求所有高度的最大值就可以了

或者直接拿 10^5 当作最大值也可以，由于所有的高度都是小于等于 10^5

输入规模为 10^5，比较大，尽量使用 scanf 来读入

const int N = 100000；

int n；
int h[ n ]；

为了防止出现边界问题，如果需要使用到 h[ n ] 这个位置，这个位置其实是 h[ n + 1 ] 这个位置，也就是第 100001 个位置，可能会发生数组越界的风险，为了避免出现数组越界的风险，多加 10 个数组位置

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
 
const int N = 100010;
 
int n;
int h[N];
 
//递推过程
bool check(int e)
{
    //从前往后递推一遍 e
    for(int i = 1;i <= n;i++ )
    {
        e = e * 2 - h[i];
        //只要在某一个时刻 e ≥ 10 w 就可以返回 true
        if(e >= 1e5) return true;
        //不满足返回 false
        if(e < 0)    return false;
    }
    //如果在整个过程中,以上两种情况都没有发生,e 一定是在 0 - 1e5 之间,一定是成立的,返回 true
    return true;
}
 
int main()
{
    //读入元素个数
    scanf("%d", &n);
    //读入所有塔的高度
    for(int i = 1;i <= n;i++ ) scanf("%d",&h[i]);
    /* 确定二分找答案的可能范围 
            答案的最小值是 0   但是不能取 0 由于初始值要保证大于等于 0 
            答案的最大值是 1e5 只要保证能量大于所有高度的最大值 能量值一定不会递减 一定都满足要求
            因此最大值取 10 w 就可以保证它大于等于所有塔的高度
    */
    int l = 0,r = 1e5;
    while(l < r) 
    {
        int mid = (l + r) >> 1;
        if(check(mid)) r = mid;
        //如果不满足 答案一定严格大于 mid
        else l = mid + 1;
    }
    //输出答案 输出 l 和 r 都是相等的
    printf("%d\n",r);
    return 0;
}

四平方和

第七届蓝桥杯省赛C++A/B组，第七届蓝桥杯省赛JAVAB/C组

 

任何一个正整数一定可以表示成至多 4 个正整数的平方和，如果把 0 包括进去，一定可以表示成 4 个数的平方和。

对于同样一个正整数而言，存在多种平方和的表示方法，要输出其中一种，把每一个方案中的四个数 a、b、c、d 按照递增的顺序来排序，输出最小的一个，对于一个四元组排序，按照字典序来比较，先看第一位是不是相同，如果第一位相同再比较第二位，输出字典序最小的一个表示法

样例

输入一个 5，输出 0 0 1 2

5 可以表示成 0^2 + 0^2 + 1^2 + 2^2

数据范围 n ＜ 500 w，考虑一个问题怎么做，最关键的就是时间复杂度的问题，需要合理设计算法使得时间是满足要求的

a、b、c、d 四个数，先考虑一下每个数的范围，由于 n 小于等于 5 × 10^6，因此每个数一定小于等于 √ n

每个数的范围大概在 0 - 2200 之间，因此我们最多可以枚举两个数，不能枚举三个数，如果枚举三个数时间复杂度为 2200^3 = 8 × 10^9，会导致超时

但是我们实际上要枚举三个数，只要枚举出 a、b、c，就可以直接计算 d

考虑用考虑换时间，枚举的时候本来要枚举三重循环，我们可以先枚举一半，把这一半的结果存储下来，先枚举 c 和 d 的所有组合，c 从 0 开始枚举，d 从 c 开始枚举，然后把所有的 c^2 + d^2 存储下来，存储的时间复杂度是 O( n^2 )，2000^2 = 500 w，再枚举 a 和 b，t 表示与最终答案的差，只需要判断 t 是否在前面枚举的 c^2 + d^2 中出现过，如果出现过，就找到了一组解，时间复杂度降为 2200^2 × O( if )

题目规定 a<=b<=c<=d，因为都是从小到大枚举的，先枚举 c，然后在 c 的基础上枚举 d，所以 c<=d，然后把它们存起来。再从 0 开始枚举先枚举 a，然后在 a 的基础上枚举 b，所以 a <= b，所以第一个找到的肯定 a 和 b 最小的，然后 c 和 d 也是最小的，直接输出就好

如何快速判断出来某一个数在某一堆数里面是不是出现过呢？一般有两种做法，一种是哈希，一种是二分

先把 c 和 d 的所有组合存储下来，再枚举 a 和 b 的所有组合，再查询差值是不是在前面出现过，如果出现过的话就找到了一组解

二分做法可以先把所有数存储到数组里面然后排序

如何找到字典序最小的解？

字典序指的是按照 a、b、c、d 的顺序比较这四个数，如果 a 相同的话再比较 b，如果 b 相同再比较 c，如果不同的话就是小的那个字典序较小

由于是从 0 开始枚举的 a，枚举的时候第一个数一定是字典序最小的，在第一个数典序最小的前提下，可以发现 b 是从 a 开始枚举，b 也是从小到大枚举的，前两个数已经保证字典序最小的，只需要找到后两个数同时最小的一个解就可以了

在存储方案的时候，不仅要找到 t 是否出现过，同时还要找到 t 的字典序最小的一个 c 和 d 的组合，将 c^2 + d^2 排序的时候要排序三个数

结构体排序：按照字典序将这三个数排序，如果第一个数不同，字典序小的那个排在前面，如果第一个数相同再看第二个数，如果第二个数相同再看第三个数

二分的时候只要找到大于等于 n - a^2 - b^2 最小的一个数就可以了，最小指的是如果值相同，字典序最小

哈希表只存储字典序最小的一个解，查询 t 的时候只需要在哈希表中查询这个值是否存在就可以了，如果存在，只保留了字典序最小的一个解

暴力做法 O( n^3 ) 超时

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
 
using namespace std;
 
const int N = 2500010;
 
int n;
 
int main()
{
    cin >> n;
    //a 从 0 开始枚举 b 从 a 开始枚举 c 从 b 开始枚举
    for (int a = 0; a * a <= n; a ++ )
        for (int b = a; a * a + b * b <= n; b ++ )
            for (int c = b; a * a + b * b + c * c <= n; c ++ )
            {
                //计算 d
                int t = n - a * a - b * b - c * c;
                int d = sqrt(t);
                //判断
                if (d * d == t)
                {
                    printf("%d %d %d %d\n", a, b, c, d);
                    return 0;
                }
            }
}

二分 O( n^2logn )

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
 
using namespace std;
 
const int N = 2500010;
 
//用一个结构体存储中间状态
struct Sum
{
    //s 表示 c^2 + d^2 
    int s, c, d;
    //排序需要重载小于号
    bool operator< (const Sum &t)const
    {
        //三关键字按字典序来比较 先比较s 如果s不同 返回s较小的那个
        if (s != t.s) return s < t.s;
        //如果s相同比较c 如果c不同 返回c较小的那个
        if (c != t.c) return c < t.c;
        //否则返回d较小的那个
        return d < t.d;
    }
}sum[N];
 
int n, m;
 
int main()
{
    //n 表示所有组合个数
    cin >> n;
    //首先按照字典序枚举 c 和 d 所有组合
    for (int c = 0; c * c <= n; c ++ )
        for (int d = c; c * c + d * d <= n; d ++ )
            //存储 第一个数是平方和
            sum[m ++ ] = {c * c + d * d, c, d};
    //排序 按照字典序比较
    sort(sum, sum + m);
    //枚举 a 和 b
    for (int a = 0; a * a <= n; a ++ )
        for (int b = 0; a * a + b * b <= n; b ++ )
        {
            //差值
            int t = n - a * a - b * b;
            //二分找大于等于差值最小的一个数
            int l = 0, r = m - 1;
            while (l < r)
            {
                int mid = l + r >> 1;
                //如果当前位置的和大于等于 t 说明答案在这个位置的左边
                if (sum[mid].s >= t) r = mid;
                else l = mid + 1;
            }
            //判断 l 这个位置是不是 t 如果是的话说明找到了一组解
            if (sum[l].s == t)
            {
                printf("%d %d %d %d\n", a, b, sum[l].c, sum[l].d);
                return 0;
            }
        }
 
    return 0;
}

哈希表 O( n^2 ) 超时

#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
 
//用 x 表示 first y 表示 second
#define x first
#define y second
 
using namespace std;
//和相同只需要存储字典序最小的一个 把一个整数映射成一个 pair
typedef pair<int, int> PII;
 
const int N = 2500010;
 
int n, m;
unordered_map<int, PII> S;
 
int main()
{
    cin >> n;
    //由于是按照字典序的顺序枚举c和d 所以只需要存第一个数 第一个数一定是字典序最小的
    for (int c = 0; c * c <= n; c ++ )
        for (int d = c; c * c + d * d <= n; d ++ )
        {
            int t = c * c + d * d;
            //判断S此时是不是有t 如果没有t才存储 
            if (S.count(t) == 0) S[t] = {c, d};
        }
 
    for (int a = 0; a * a <= n; a ++ )
        for (int b = 0; a * a + b * b <= n; b ++ )
        {
            int t = n - a * a - b * b;
            //如果S当中存在t说明找到答案直接输出
            if (S.count(t))
            {
                printf("%d %d %d %d\n", a, b, S[t].x, S[t].y);
                return 0;
            }
        }
 
    return 0;
}

二分比哈希表慢 logn 倍，log 500 w 大概等于 20 倍，所以从理论上来说，二分比哈希慢 20 倍左右，但此时发现哈希表的运行效率比二分慢一倍，由于常数不一样，虽然哈希表的时间复杂度是 O( 1 )，但是有可能每一个 O( 1 ) 里面都要执行 20 次操作，所以哈希表的常数比二分慢 40 倍左右

分巧克力

第八届蓝桥杯省赛C++A/B组,第八届蓝桥杯省赛JAVAA/B组

有 k 位小朋友来做客，小明一共有 n 块巧克力，每一块巧克力都是 h × w 的长方形，h 是高度，w 是宽度，为了公平起见，小明需要从这 n 块巧克力中切出 k 块巧克力分给小朋友

切出的巧克力需要满足：

        1.形状是正方形，边长是整数

        2.大小相同

6 × 5 的巧克力只能切两块 3 × 3 的，或者切三块 2 × 2 的

当然小朋友们都希望得到的巧克力尽可能大，在切出来 k 块巧克力的前提下，要求计算出每一块巧克力边长最大值是多少？

只能裁剪不能拼接，很容易可以想到用二分来求解

if( f( mid ) ≥ k )  成立，说明所有满足 ＜ mid 的边长也一定是可以满足要求的，并且 mid 本身也一定是可以满足要求的，当前答案一定是在 mid 或者 大于等于 mid 的位置，在更新的时候应该是 L = mid，如果当前边长不能满足 k，说明答案一定比 k 更小，而且 mid 不能作为答案，在更新的时候应该是 R = mid - 1

下图给出函数，横坐标是切的边长，纵坐标是切的块数，可以发现一定是一个递减函数

其实每一块巧克力能切多少块是可以计算出来的，假设当前这块巧克力的边长是 Wi × Hi，如果我们想切出来边长是 x 的巧克力的话，能切的块数如下

对于每一块巧克力来说能切出来的小正方形巧克力的数量是随着边长的增大而递减，x 增大，Wi / x 一定递减

要找到一个满足块数大于等于 k 的最大的边长，如果答案是 x0，所有 ≤ x0 的边长一定可以切出来 k 块，因此一定是可以二分的

时间复杂度分析

求 f( mid ) 需要扫描一遍巧克力块，时间复杂度为 O( n )，二分 logH 次

 

输入保证每位小朋友至少能获得一块 1×1 的巧克力，数据保证了答案一定是大于等于 1

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
 
using namespace std;
 
const int N = 100010;
 
int n,k;
//h 表示每一块巧克力的高度 w 表示每一块巧克力的长度
int h[N],w[N];
 
bool check(int mid)
{
    //res 表示一共可以分多少块
    int res = 0;
    //枚举每一个完整的巧克力
    for(int i = 0;i < n;i++ )
    {
        //注意加上括号
        res += (h[i] / mid) * (w[i] / mid);
        //如果发现 res >= k 就可以返回 true
        if(res >= k) return true;
    }
    //如果枚举完之后都没有发现 res ≥ k 说明不满足要求返回 false 
    return false;
}
 
int main()
{
    scanf("%d%d",&n, &k);
    //读入每一块巧克力的初始长度
    for(int i = 0;i < n;i++ ) scanf("%d%d",&h[i],&w[i]);
    //二分答案的长度 最小值从 1 开始取,最大值不能超过 h 和 w,如果超过所有 h 和 w,答案就是 0,但是保证答案最小是 1
    int l = 1,r = 1e5;
    while(l < r)
    {
        int mid = l + r + 1 >> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }
    //最终 l 等于 r 输出 l 和 r 都一样
    printf("%d\n",r);
    return 0;
}