• 【王道数据结构编程题】- 二叉树算法练习

    目录

    1.假设二叉树采用二叉链存储结构存储，设计一个算法，求先序遍历序列中第k(1<=k<=二叉树中节点个数)个节点的值。

    2.已知二叉树以二叉链表存储，编写算法完成，对于树中每个元素值为x的节点，删去以它为根的子树，并且释放相应的空间。

    3.在二叉树中查找值为x的节点，试编写算法打印值为x的节点的所有祖先，假设值为x的节点不多于1个。

    4.编写算法找到p和q的最近公共祖先。

    5.设计算法，求非空二叉树的宽度。

    6.设一颗满二叉树，已知其先序序列，设计算法求其后序序列

    7.设计算法将二叉树的叶节点按从左到右的顺序连成一个单链表。

    8.设计算法判断两个二叉树是否相似。

    1.假设二叉树采用二叉链存储结构存储，设计一个算法，求先序遍历序列中第k(1<=k<=二叉树中节点个数)个节点的值。

    1. //假设二叉树采用二叉链表存储结构存储，设计一个算法
    2. //求先序遍历序列中第k(1<=k<=二叉树中节点个数)个节点的值
    3. #include<iostream>
    4. using namespace std;
    5. //结构体
    6. typedef struct treenode{
    7.     //节点的值
    8. 	char data;
    9. 	//节点的左右孩子指针
    10. 	struct treenode *lchild,*rchild;
    11. }treenode,*tree;
    12.  
    13. //建树 赋值节点
    14. void buildtree(tree &t)
    15. {
    16. 	char ch;
    17. 	ch = getchar();
    18. 	if(ch=='#') t=NULL;
    19. 	else
    20. 	{
    21. 		//对节点进行内存分配
    22. 		t=(treenode *)malloc(sizeof(treenode));
    23. 		//对节点进行赋值
    24. 		t->data=ch;
    25. 		//初始化 左右孩子节点为空
    26. 		t->lchild=NULL;
    27. 		t->rchild=NULL;
    28. 		//递归去赋值左右子树
    29. 		buildtree(t->lchild);
    30. 		buildtree(t->rchild);
    31. 	}
    32. }
    33.  
    34. //先序遍历 递归
    35.  
    36. //计数器
    37. int i=1;
    38. //字符
    39. char ch;
    40. char PreNode(tree t ,int k)
    41. {
    42. 	if(t==NULL) return '#';
    43. 	if(i==k) return t->data;
    44. 	i++;
    45. 	ch = PreNode(t->lchild,k);
    46. 	if(ch!='#') return ch;
    47. 	ch = PreNode(t->rchild,k);
    48. 	return ch;
    49. }
    50.  
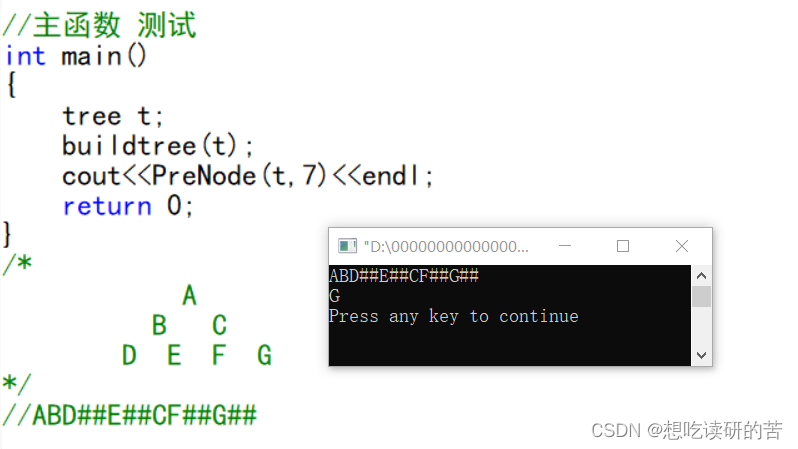
    51. //主函数 测试
    52. int main()
    53. {
    54. 	tree t;
    55. 	buildtree(t);
    56. 	cout<<PreNode(t,7)<<endl;
    57. 	return 0;
    58. }
    59. /*
    60.             A
    61. 	      B   C
    62. 		D  E  F  G
    63. */
    64. //ABD##E##CF##G##

    2.已知二叉树以二叉链表存储，编写算法完成，对于树中每个元素值为x的节点，删去以它为根的子树，并且释放相应的空间。

    1. //已知二叉树以二叉链表存储，编写算法完成 
    2. //对于树中每个元素值为x的节点，删去以它为根的子树，并释放相应的空间
    3. #include<iostream>
    4. using namespace std;
    5. //结构体
    6. typedef struct treenode{
    7.     //节点的值
    8. 	char data;
    9. 	//节点的左右孩子指针
    10. 	struct treenode *lchild,*rchild;
    11. }treenode,*tree;
    12.  
    13. //建树 赋值节点
    14. void buildtree(tree &t)
    15. {
    16. 	char ch;
    17. 	ch = getchar();
    18. 	if(ch=='#') t=NULL;
    19. 	else
    20. 	{
    21. 		//对节点进行内存分配
    22. 		t=(treenode *)malloc(sizeof(treenode));
    23. 		//对节点进行赋值
    24. 		t->data=ch;
    25. 		//初始化 左右孩子节点为空
    26. 		t->lchild=NULL;
    27. 		t->rchild=NULL;
    28. 		//递归去赋值左右子树
    29. 		buildtree(t->lchild);
    30. 		buildtree(t->rchild);
    31. 	}
    32. }
    33.  
    34. //递归释放节点
    35. void Release(tree &t)
    36. {
    37. 	if(!t) return;
    38. 	Release(t->lchild);
    39.     Release(t->rchild);
    40. 	free(t);
    41. }
    42.  
    43. //前序序列
    44. void delete_x(tree &T,char x)
    45. {
    46. 	if(T==NULL) return;
    47. 	if(T->data==x)
    48. 	{
    49. 		//递归释放节点
    50.         Release(T);
    51. 		//手动去设置节点为NULL，物理内存的一个释放
    52. 		T=NULL;
    53. 	}
    54. 	if(T!=NULL)
    55. 	{
    56. 		delete_x(T->lchild,x);
    57. 		delete_x(T->rchild,x);
    58. 	}
    59. }
    60.  
    61. //打印
    62. void disp(tree t)
    63. {
    64. 	if(t)
    65. 	{
    66. 		cout<<t->data<<" ";
    67. 		disp(t->lchild);
    68. 		disp(t->rchild);
    69. 	}
    70. }
    71.  
    72. //主函数 测试
    73. int main()
    74. {
    75. 	tree t;
    76. 	buildtree(t);
    77. 	delete_x(t,'C');
    78. 	disp(t);
    79. 	return 0;
    80. }
    81. /*
    82.             A
    83. 	      B   C
    84. 		D  E  F  G
    85. */
    86. //ABD##E##CF##G##

    3.在二叉树中查找值为x的节点，试编写算法打印值为x的节点的所有祖先，假设值为x的节点不多于1个。

    1. //在二叉树中查找值为x的节点，试着编写算法
    2. //打印值为x的节点的所有祖先，假设值为x的节点不多于1个
    3. #include<iostream>
    4. using namespace std;
    5. //树节点结构体
    6. typedef struct treenode{
    7.     //节点的值
    8. 	char data;
    9. 	//节点的左右孩子指针
    10. 	struct treenode *lchild,*rchild;
    11. }treenode,*tree;
    12.  
    13. //节点栈的结构体
    14. typedef struct{
    15.    //树的节点
    16. 	treenode *t;
    17. 	//此节点的左右孩子访问变量 tag=0 左孩子已经访问过 =1 右孩子已经访问过
    18. 	int tag;
    19. }Stack;
    20.  
    21. //建树 赋值节点
    22. void buildtree(tree &t)
    23. {
    24. 	char ch;
    25. 	ch = getchar();
    26. 	if(ch=='#') t=NULL;
    27. 	else
    28. 	{
    29. 		//对节点进行内存分配
    30. 		t=(treenode *)malloc(sizeof(treenode));
    31. 		//对节点进行赋值
    32. 		t->data=ch;
    33. 		//初始化 左右孩子节点为空
    34. 		t->lchild=NULL;
    35. 		t->rchild=NULL;
    36. 		//递归去赋值左右子树
    37. 		buildtree(t->lchild);
    38. 		buildtree(t->rchild);
    39. 	}
    40. }
    41.  
    42. //非递归后序遍历
    43. void grand(tree t,char x)
    44. {
    45. 	//栈 栈的栈顶指针top的初始化指向 0
    46. 	Stack s[10];
    47. 	int top = 0;
    48. 	while(t!=NULL||top>0)
    49. 	{
    50. 		//从根节点开始向左延深压入栈中并且节点的值不为x
    51. 		while(t!=NULL&&t->data!=x)
    52. 		{
    53. 			s[++top].t=t;
    54. 			s[top].tag=0;
    55. 			t=t->lchild;
    56. 		}
    57. 		//如果找到了值为x的节点 将栈中的节点值输出
    58. 		if(t!=NULL&&t->data==x)
    59. 		{
    60. 			printf("所有的祖先节点为:\n");
    61. 			for(int i=1;i<=top;i++)
    62. 			{
    63. 				printf("%c\n",s[i].t->data);
    64. 			}
    65. 		}
    66. 		//判断当前栈顶的节点的tag值 为1 的话 依次退栈
    67. 		while(top!=0&&s[top].tag==1)
    68. 		{
    69. 			top--;
    70. 		}
    71. 		//当前栈顶不为0 将栈顶的tag值赋值为1 节点指向该节点的右孩子
    72. 		if(top!=0)
    73. 		{
    74. 			s[top].tag=1;
    75. 			t=s[top].t->rchild;
    76. 		}
    77. 	}
    78. }
    79.  
    80. //主函数 测试
    81. int main()
    82. {
    83. 	tree t;
    84. 	buildtree(t);
    85. 	grand(t,'D');
    86. 	return 0;
    87. }
    88. /*
    89.             A
    90. 	      B   C
    91. 		D  E  F  G
    92. */
    93. //ABD##E##CF##G##

    4.编写算法找到p和q的最近公共祖先。

    1. //找到p和q的最近公共祖先节点
    2. #include<iostream>
    3. using namespace std;
    4. //树节点结构体
    5. typedef struct treenode{
    6.     //节点的值
    7. 	char data;
    8. 	//节点的左右孩子指针
    9. 	struct treenode *lchild,*rchild;
    10. }treenode,*tree;
    11.  
    12. //节点栈的结构体
    13. typedef struct{
    14.    //树的节点
    15. 	treenode *t;
    16. 	//此节点的左右孩子访问变量 tag=0 左孩子已经访问过 =1 右孩子已经访问过
    17. 	int tag;
    18. }Stack;
    19.  
    20. //建树 赋值节点
    21. void buildtree(tree &t)
    22. {
    23. 	char ch;
    24. 	ch = getchar();
    25. 	if(ch=='#') t=NULL;
    26. 	else
    27. 	{
    28. 		//对节点进行内存分配
    29. 		t=(treenode *)malloc(sizeof(treenode));
    30. 		//对节点进行赋值
    31. 		t->data=ch;
    32. 		//初始化 左右孩子节点为空
    33. 		t->lchild=NULL;
    34. 		t->rchild=NULL;
    35. 		//递归去赋值左右子树
    36. 		buildtree(t->lchild);
    37. 		buildtree(t->rchild);
    38. 	}
    39. }
    40.  
    41. //非递归后序遍历
    42. tree Ancestor(tree t,treenode *p,treenode *q)
    43. {
    44. 	//两个辅助栈
    45. 	Stack S1[10],S2[10];
    46. 	//栈顶指针的初始化
    47. 	int top1=0,top2;
    48. 	//遍历二叉树指针
    49. 	treenode *tt=t;
    50. 	//大循环体条件：当前遍历的节点不能为空或者栈1顶指针>0(栈不为空)
    51. 	while(tt!=NULL||top1>0)
    52. 	{
    53. 		//向左延伸压入栈
    54. 		while(tt!=NULL)
    55. 		{
    56. 			S1[++top1].t=tt;//压入栈中
    57. 			S1[top1].tag=0;//左孩子访问过
    58. 			tt=tt->lchild;//继续指向左孩子
    59. 		}
    60. 		while(top1!=0&&S1[top1].tag==1)//栈1不为空并且栈顶节点的tag=1
    61. 		{
    62. 			//如果栈顶的节点就是p 就复制到栈2中 栈2的栈顶指针此时赋值 top1
    63. 			if(S1[top1].t==p)
    64. 			{
    65. 				for(int i=1;i<top1;i++)
    66. 				{
    67. 					S2[i]=S1[i];
    68. 				}
    69. 				top2=top1;
    70. 			}
    71. 			//如果栈顶的节点就是q 与栈1进行匹配
    72. 			if(S1[top1].t==q)
    73. 			{
    74. 				for(int i=top1;i>0;i--)
    75. 				{
    76. 					for(int j=top2;j>0;j--)
    77. 					{
    78. 						if(S2[j].t==S1[i].t)
    79. 							return S1[i].t;
    80. 					}
    81. 				}
    82. 			}
    83. 			top1--;//退栈
    84. 		}
    85. 		//栈不为空 将栈顶节点的tag=1 并且当前的一个节点指向该节点的右孩子
    86. 		if(top1!=0)
    87. 		{
    88. 			S1[top1].tag=1;
    89. 			tt=S1[top1].t->rchild;
    90. 		}
    91. 	}
    92. 	return NULL;
    93. }
    94.  
    95. //主函数 测试
    96. int main()
    97. {
    98. 	tree t;
    99. 	buildtree(t);
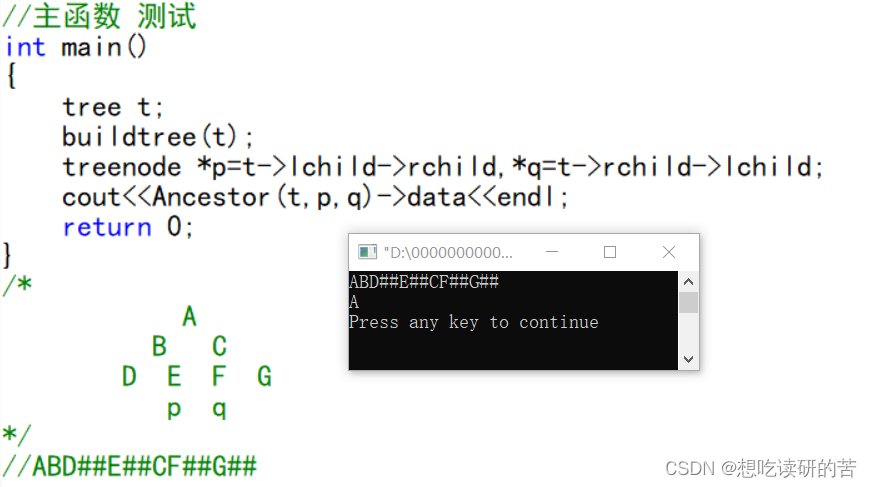
    100. 	treenode *p=t->lchild->rchild,*q=t->rchild->lchild;
    101. 	cout<<Ancestor(t,p,q)->data<<endl;
    102. 	return 0;
    103. }
    104. /*
    105.             A
    106. 	      B   C
    107. 		D  E  F  G
    108. 		   p  q
    109. */
    110. //ABD##E##CF##G##

    5.设计算法，求非空二叉树的宽度。

    1. //非空二叉树b的高度
    2. #include<iostream>
    3. using namespace std;
    4. //树节点结构体
    5. typedef struct treenode{
    6.     //节点的值
    7. 	char data;
    8. 	//节点的左右孩子指针
    9. 	struct treenode *lchild,*rchild;
    10. }treenode,*tree;
    11.  
    12. //节点队列的结构体
    13. typedef struct{
    14.   tree data[10];
    15.   int level[10];
    16.   int f,r;
    17. }Qu;
    18.  
    19. //建树 赋值节点
    20. void buildtree(tree &t)
    21. {
    22. 	char ch;
    23. 	ch = getchar();
    24. 	if(ch=='#') t=NULL;
    25. 	else
    26. 	{
    27. 		//对节点进行内存分配
    28. 		t=(treenode *)malloc(sizeof(treenode));
    29. 		//对节点进行赋值
    30. 		t->data=ch;
    31. 		//初始化 左右孩子节点为空
    32. 		t->lchild=NULL;
    33. 		t->rchild=NULL;
    34. 		//递归去赋值左右子树
    35. 		buildtree(t->lchild);
    36. 		buildtree(t->rchild);
    37. 	}
    38. }
    39.  
    40. //层次遍历
    41. int width(tree b)
    42. {
    43. 	//队列
    44. 	Qu Q;
    45. 	//出队节点的指向
    46. 	tree p;
    47. 	//保存出队的节点层次
    48. 	int k;
    49. 	//头尾指针初始化
    50. 	Q.f=Q.r=-1;
    51. 	//尾指针后移用来根节点入队
    52. 	Q.r++;
    53. 	//根节点入队
    54. 	Q.data[Q.r]=b;
    55. 	//根节点层次为1
    56. 	Q.level[Q.r]=1;
    57. 	//循环体 头指针小于尾指针可以执行
    58. 	while(Q.f<Q.r)
    59. 	{
    60. 	   //头指针后移出队
    61. 		Q.f++;
    62.        //保存出队节点
    63. 		p=Q.data[Q.f];
    64. 	   //保存出队节点的层次
    65. 		k=Q.level[Q.f];
    66. 	   //左孩子进入队列
    67. 		if(p->lchild!=NULL)
    68. 		{
    69. 			//尾指针后移 用来入队
    70. 			Q.r++;
    71. 	        //左孩子进入队列
    72. 			Q.data[Q.r]=p->lchild;
    73. 	        //进入队列的节点的层次为出队节点的层次+1
    74. 			Q.level[Q.r]=k+1;
    75. 		}
    76. 		if(p->rchild!=NULL)//右孩子进队
    77. 		{
    78. 			//尾指针后移，用来入队
    79. 			Q.r++;
    80. 			//右孩子进入队列
    81. 			Q.data[Q.r]=p->rchild;
    82. 			//进入队列的节点的层次为出队节点的层次+1
    83. 			Q.level[Q.r]=k+1;
    84. 		}
    85. 	}
    86. 	//循环遍历的时候最大值的更新，遍历下标，计算每层的个数
    87. 	int maxx=0,i=0,n;
    88. 	//从第一层开始
    89. 	k=1;
    90. 	//循环条件 遍历的下标小于队列尾部
    91.     while(i<=Q.r)
    92. 	{
    93. 		//一开始每层默认0个
    94. 		n=0;
    95. 		//当下标小于队列长度并且遍历的下标对应的层次为k的时候
    96. 		while(i<=Q.r&&Q.level[i]==k)
    97. 		{
    98. 			//每层个数递增
    99. 			n++;
    100. 			//遍历的下标后移
    101. 			i++;
    102. 		}
    103. 		//下一层的层次
    104. 		k=Q.level[i];
    105. 		//更新最大值
    106. 		if(n>maxx) maxx=n;
    107. 	}
    108. 	return maxx;
    109. }
    110. //主函数 测试
    111. int main()
    112. {
    113. 	tree t;
    114. 	buildtree(t);
    115. 	cout<<width(t)<<endl;
    116. 	return 0;
    117. }
    118. /*
    119.             A
    120. 	      B   C
    121. 		D  E  F  G
    122. */
    123. //ABD##E##CF##G##

    6.设一颗满二叉树，已知其先序序列，设计算法求其后序序列

    1. //已知先序序列，设计算法求其后序序列
    2. #include<iostream>
    3. using namespace std;
    4.  
    5. //递归交换过程
    6. void PrePost(char pre[],int l1,int h1,char post[],int l2,int h2)
    7. {
    8. 	int half;//左右子树临界
    9. 	if(l1<=h1)//递归条件
    10. 	{
    11. 		post[h2]=pre[l1];
    12. 		half=(h1-l1)/2;
    13. 		PrePost(pre,l1+1,l1+half,post,l2,l2+half-1);
    14. 	    PrePost(pre,l1+half+1,h1,post,l2+half,h2-1);
    15. 	}
    16. }
    17.  
    18. //主函数 测试
    19. int main()
    20. {
    21. 	char pre[8]="ABDECFG",post[8];
    22. 	PrePost(pre,0,6,post,0,6);
    23. 	for(int i=0;i<7;i++)
    24. 	{
    25. 		cout<<post[i]<<" ";
    26. 	}
    27. 	return 0;
    28. }
    29.  
    30. /*
    31.             A
    32. 	      B   C
    33. 		D  E  F  G
    34. */
    35. //ABD##E##CF##G##

    7.设计算法将二叉树的叶节点按从左到右的顺序连成一个单链表。

    1. //叶节点从左到右连接成单链表
    2. #include<iostream>
    3. using namespace std;
    4.  
    5. //树节点结构体
    6. typedef struct treenode{
    7.     //节点的值
    8. 	char data;
    9. 	//节点的左右孩子指针
    10. 	struct treenode *lchild,*rchild;
    11. }treenode,*tree;
    12.  
    13. //建树 赋值节点
    14. void buildtree(tree &t)
    15. {
    16. 	char ch;
    17. 	ch = getchar();
    18. 	if(ch=='#') t=NULL;
    19. 	else
    20. 	{
    21. 		//对节点进行内存分配
    22. 		t=(treenode *)malloc(sizeof(treenode));
    23. 		//对节点进行赋值
    24. 		t->data=ch;
    25. 		//初始化 左右孩子节点为空
    26. 		t->lchild=NULL;
    27. 		t->rchild=NULL;
    28. 		//递归去赋值左右子树
    29. 		buildtree(t->lchild);
    30. 		buildtree(t->rchild);
    31. 	}
    32. }
    33.  
    34. //全局 头节点 前驱节点 类型仍然是树节点的一个结构体 通过rchild连接
    35. tree head = (treenode *)malloc(sizeof(treenode)),pre=NULL;
    36.  
    37. //中序遍历
    38. tree Inorder(tree t)
    39. {
    40. 	//递归条件 节点不为空
    41. 	if(t)
    42. 	{
    43. 		//将根节点左孩子作为参数 一直递归向左延申
    44. 		Inorder(t->lchild);
    45. 		//找到叶子节点
    46. 		if(t->lchild==NULL&&t->rchild==NULL)
    47. 		{
    48. 			//如果是第一个
    49. 			if(pre==NULL)
    50. 			{
    51. 				//头节点赋值
    52. 				head = t;
    53. 				/*保留前驱节点 前驱节点为当前的一个节点 保证后面再次遇到叶子节点的时候知道
    54. 				前驱节点是谁 并且能够进行连接*/
    55. 				pre=t;
    56. 			}
    57. 			//若不是第一个
    58. 			else
    59. 			{
    60. 				//就将前驱节点的右指针指向当前的节点
    61. 				pre->rchild=t;
    62. 				//更新前驱节点 保证后面再次遇到叶子节点的时候知道前驱节点是谁 并且能够连接
    63. 				pre=t;
    64. 			}
    65. 		}
    66. 		//左子树递归完成了 向左递归右子树
    67. 		Inorder(t->rchild);
    68. 		//右子树递归完后可以将最后一个节点也就是更新后的前驱节点的右指针指向空
    69. 		pre->rchild=NULL;
    70. 	}
    71. 	//最后返回头节点即可 可以通过头节点来遍历整个节点链
    72. 	return head;
    73. }
    74.  
    75. //主函数 测试
    76. int main()
    77. {
    78. 	tree t;
    79. 	buildtree(t);
    80. 	Inorder(t);
    81. 	while(head)
    82. 	{
    83. 		cout<<head->data<<" ";
    84. 		head = head->rchild;
    85. 	}
    86. 	return 0;
    87. }
    88. /*
    89.             A
    90. 	      B   C
    91. 		D  E  F  G
    92. */
    93. //ABD##E##CF##G##

    8.设计算法判断两个二叉树是否相似。

    1. //两颗二叉树是否相似
    2. #include<iostream>
    3. using namespace std;
    4.  
    5. //树节点结构体
    6. typedef struct treenode{
    7.     //节点的值
    8. 	char data;
    9. 	//节点的左右孩子指针
    10. 	struct treenode *lchild,*rchild;
    11. }treenode,*tree;
    12.  
    13. //建树 赋值节点
    14. void buildtree(tree &t)
    15. {
    16. 	char ch;
    17. 	cin>>ch;
    18. 	if(ch=='#') t=NULL;
    19. 	else
    20. 	{
    21. 		//对节点进行内存分配
    22. 		t=(treenode *)malloc(sizeof(treenode));
    23. 		//对节点进行赋值
    24. 		t->data=ch;
    25. 		//初始化 左右孩子节点为空
    26. 		t->lchild=NULL;
    27. 		t->rchild=NULL;
    28. 		//递归去赋值左右子树
    29. 		buildtree(t->lchild);
    30. 		buildtree(t->rchild);
    31. 	}
    32. }
    33.  
    34. //递归比较左右子树 空+空->1  空+非空->0
    35. int similar(tree t1,tree t2)
    36. {
    37. 	int left,right;
    38. 	if(t1==NULL&&t2==NULL) {return 1;}
    39. 	else if(t1==NULL||t2==NULL) {return 0;}
    40. 	else
    41. 	{
    42. 		left = similar(t1->lchild,t2->lchild);
    43. 		right = similar(t1->rchild,t2->rchild);
    44. 		return(left&&right);
    45. 	}
    46. }
    47.  
    48. //主函数 测试
    49. int main()
    50. {
    51. 	tree t1,t2;
    52. 	buildtree(t1);
    53.     buildtree(t2);
    54.     cout<<similar(t1,t2)<<endl;
    55. 	return 0;
    56. }
    57.  
    58. /*
    59.       A
    60. 	B
    61.   测试t1:AB###
    64.   C
    65.     E
    66.   测试t2:C#E##
    67. */

  • 相关阅读:
    从实时应用角度谈通信总线仲裁机制和网络流控
    《Vue入门到精通系列之四》--- vue cli详解
    彻底理解Java并发：volatile关键字
    【Gzip】详细介绍
    Redis发布订阅机制学习
    Jetson Xavier NX 平台gstreamer elements 在Jetpack 5.0.2更慢比Jetpack 4.6
    直播的多样性
    如此理解sed会简单
    Javaweb03-servlet&filter
    【IPC 通信】信号处理接口 Signal API（5）
  • 原文地址：https://blog.csdn.net/m0_56051805/article/details/125418146