MKL库矩阵乘法(cblas_dgemm)

MKL库中基本线性代数子程序，BLAS(Basic Linear Algebra Subprograms)库，是一个API标淮，用以规范发布基础线性代数操作的数值库（如向量或矩阵乘法）。其中CBLAS是BLAS的C语言接口。

库中前缀用来区分所支持处理的数据类型。

前缀	描述	函数名系列	描述
s-	实数、单精度	ge...	一般矩阵
c-	复数、单精度	sy...	对称矩阵
d-	实数、双精度	he...	Hermitian矩阵
z-	复数、双精度	tr...	三角矩阵

基本矩阵、向量操作

函数（采用常规的前缀为d的接口）	描述
cblas_dasum	向量元素值模的总和
cblas_daxpy	缩放向量
cblas_dcopy	复制向量
cblas_ddot	向量点积
cblas_dswap	交换两向量
cblas_dgemv	常规矩阵×向量

重点介绍矩阵的乘法运算。

此示例是利用Intel 的MKL库函数完成计算矩阵（乘法）运算，计算式为：

C=α∗A∗B+β∗C

其通过调整A、B、C矩阵及其系数，同样可以完成矩阵的加减；如若只需矩阵A与B的乘积，设置α=1,β=0即可。

其中A为m×k维矩阵，B为k×n维矩阵，C为m×n维矩阵。

使用的函数为cblas_dgemm(Double precision GEneric Matrix Multiplication)，完成一般的矩阵乘法。

1 cblas_dgemm参数详解

fun cblas_dgemm(Layout,		//指定行优先(CblasRowMajor,C)或列优先(CblasColMajor,Fortran)数据排序
               TransA,		//指定是否转置矩阵A
               TransB,		//指定是否转置矩阵B
               M,		//矩阵A和C的行数
               N,		//矩阵B和C的列数
               K,		//矩阵A的列，B的行
               alpha,		//矩阵A和B乘积的比例因子
               A,		//A矩阵
               lda,		//矩阵A的第一维的大小
               B,		//B矩阵
               ldb,		//矩阵B的第一维的大小
               beta,		//矩阵C的比例因子
               C,		//(input/output) 矩阵C
               ldc		//矩阵C的第一维的大小
               )		

2 定义待处理矩阵

#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"		// 调用mkl头文件

#define min(x,y) (((x) < (y)) ? (x) : (y))	

double* A, * B, * C;		//声明三个矩阵变量，并分配内存
int m, n, k, i, j;			//声明矩阵的维度，其中
double alpha, beta;

m = 2000, k = 200, n = 1000;
alpha = 1.0; beta = 0.0;

A = (double*)mkl_malloc(m * k * sizeof(double), 64);	//按照矩阵维度分配内存
B = (double*)mkl_malloc(k * n * sizeof(double), 64);	//mkl_malloc用法与malloc相似，64表示64位
C = (double*)mkl_malloc(m * n * sizeof(double), 64);
if (A == NULL || B == NULL || C == NULL) {		//判空

    mkl_free(A);				
    mkl_free(B);
    mkl_free(C);
    return 1;
}

for (i = 0; i < (m * k); i++) {		//赋值
    A[i] = (double)(i + 1);
}

for (i = 0; i < (k * n); i++) {
    B[i] = (double)(-i - 1);
}

for (i = 0; i < (m * n); i++) {
    C[i] = 0.0;
}

其中A和B矩阵设置为：

A=[1.02.0⋯1000.01001.01002.0⋯2000.0⋮⋮⋱⋯999001.0999002.0⋯1000000.0] B=[−1.0−2.0⋯−1000.0−1001.0−1002.0⋯−2000.0⋮⋮⋱⋯−999001.0−999002.0⋯−1000000.0]

C矩阵为全0。

3 执行矩阵乘法

回到例子中，对照上面的参数，将C矩阵用A与B的矩阵乘法表示：

cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, m, n, k, alpha, A, k, B, n, beta, C, n);

执行后的得到结果如下：

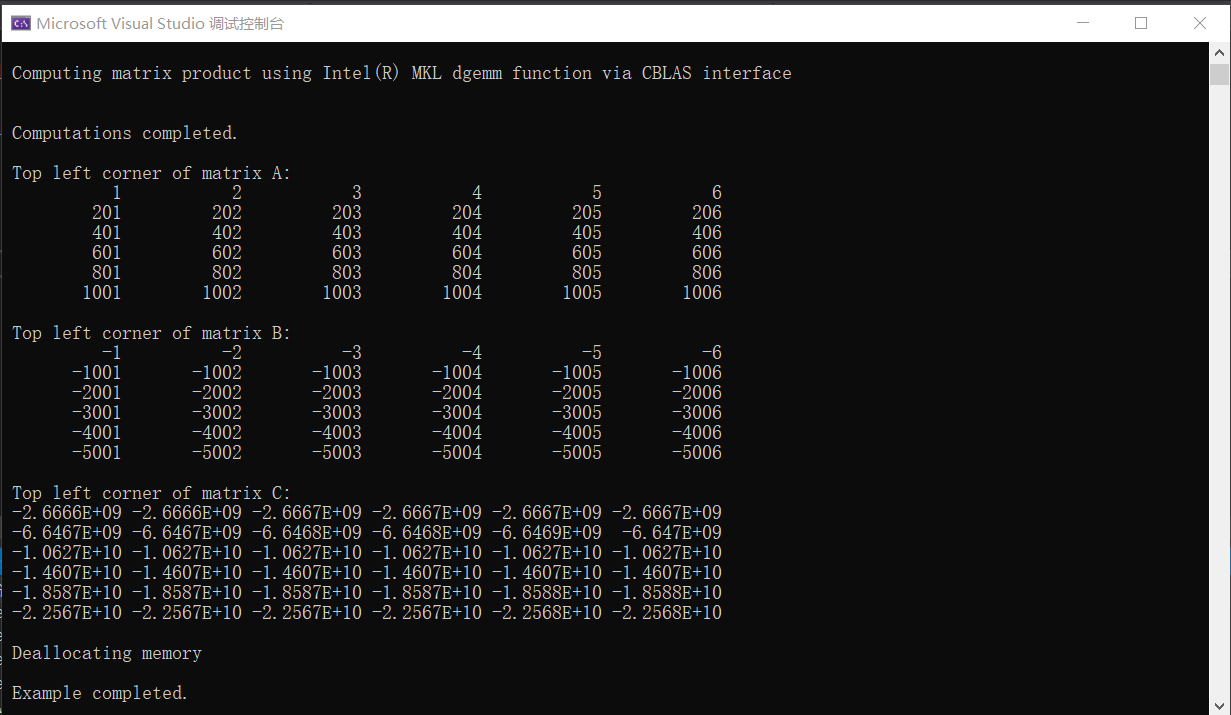
完整代码

#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"

#define min(x,y) (((x) < (y)) ? (x) : (y))

int main()
{
    double* A, * B, * C;
    int m, n, k, i, j;
    double alpha, beta;


    m = 2000, k = 200, n = 1000;

    alpha = 1.0; beta = 0.0;

    A = (double*)mkl_malloc(m * k * sizeof(double), 64);
    B = (double*)mkl_malloc(k * n * sizeof(double), 64);
    C = (double*)mkl_malloc(m * n * sizeof(double), 64);
    if (A == NULL || B == NULL || C == NULL) {

        mkl_free(A);
        mkl_free(B);
        mkl_free(C);
        return 1;
    }


    for (i = 0; i < (m * k); i++) {
        A[i] = (double)(i + 1);
    }

    for (i = 0; i < (k * n); i++) {
        B[i] = (double)(-i - 1);
    }

    for (i = 0; i < (m * n); i++) {
        C[i] = 0.0;
    }

    cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
        m, n, k, alpha, A, k, B, n, beta, C, n);


    for (i = 0; i < min(m, 6); i++) {
        for (j = 0; j < min(k, 6); j++) {
            printf("%12.0f", A[j + i * k]);
        }
        printf("\n");
    }

    for (i = 0; i < min(k, 6); i++) {
        for (j = 0; j < min(n, 6); j++) {
            printf("%12.0f", B[j + i * n]);
        }
        printf("\n");
    }

    for (i = 0; i < min(m, 6); i++) {
        for (j = 0; j < min(n, 6); j++) {
            printf("%12.5G", C[j + i * n]);
        }
        printf("\n");
    }

    mkl_free(A);
    mkl_free(B);
    mkl_free(C);

    return 0;
}