排序方法——《快速排序》

P. S.：以下代码均在VS2019环境下测试，不代表所有编译器均可通过。 P. S.：测试代码均未展示头文件stdio.h的声明，使用时请自行添加。
  

                                           博主主页：Yan. yan.
                                              C语言专栏
                                            数据结构专栏
                                         力扣牛客经典题目专栏

一、快速排序的定义

  快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：
  任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

  快速排序分为两种： 递归法    非递归

  递归法又分为三种： hoare法  双指针法 挖坑法

二、快速排序的递归方法实现

1、hoare法

  hoare法的动图展示：

  起主要思想为：循环遍历数组元素

• 定义三个变量：key，begin 和 end，其中 key 和 begin 指向数组首元素，end 指向数组尾元素
• begin 从右边开始寻找比 key 小的值， end 从左边开始寻找比 key 大的值，两者找到相应的值以后再将各自的值进行交换，直到二者相遇。
• 如果begin 和 end 相遇了，那么将相遇位置的值与 key 位置的值进行交换。
• 将交换后的key的位置记录下来作为新的分割点， 再以相同的方法递归key左边和右边的元素

  完整代码展示：

void Swap(int* a, int* b)
{
	int ret = *a;
	*a = *b;
	*b = ret;
}

//快速排序  hoare
void QuickSort(int* arr, int left, int right)
{
	if (left >= right)
		return;

	int key = left;
	int begin = left;
	int end = right;

	while (begin < end)
	{
		while (begin < end && arr[end] >= arr[key])
		{
			end--;
		}
		while (begin < end && arr[begin] <= arr[key])
		{
			begin++;
		}
		Swap(&arr[begin], &arr[end]);
	}
	Swap(&arr[begin], &arr[key]);
	key = begin;

	QuickSort(arr, left, key - 1);
	QuickSort(arr, key + 1, right);
}

2、双指针法

  双指针法的动图展示：

  其主要思想为：

• 定义三个变量：key prve cur，对应数组下标，key 和 prve 指向首元素下标，cur 指向prve 的下一个元素下标。
• 如果cur位置的值小于key，那么prve++，然后将prve处的值与cur位置的值进行交换，再cur++
• 如果cur位置的值大于key，那么cur++，直到找到小于key的值
• 如果cur已经走出了数组（cur > right）那么就让prve处的值与key处的值交换
• 将交换后的key的位置记录下来作为新的分割点， 再以相同的方法递归key左边和右边的元素

  完整代码展示：

void Swap(int* a, int* b)
{
	int ret = *a;
	*a = *b;
	*b = ret;
}

//快速排序  双指针法
void QuickSort(int* arr, int left, int right)
{
	if (left >= right)
		return;

	int key = left;
	int prve = left;
	int cur = prve + 1;
	while (cur <= right)
	{
		if (arr[cur] <= arr[key] && ++prve != cur)//这里如果prve++后与cur在同一位置，自己与自己交换没有意义，所以多加一个判断条件
		{                                
			Swap(&arr[prve], &arr[cur]);
		}
		cur++;
	}
	Swap(&arr[prve], &arr[key]);
	key = prve;

	QuickSort(arr, left, key - 1);
	QuickSort(arr, key + 1, right);
}

3、挖坑法

  挖坑法的动图展示：

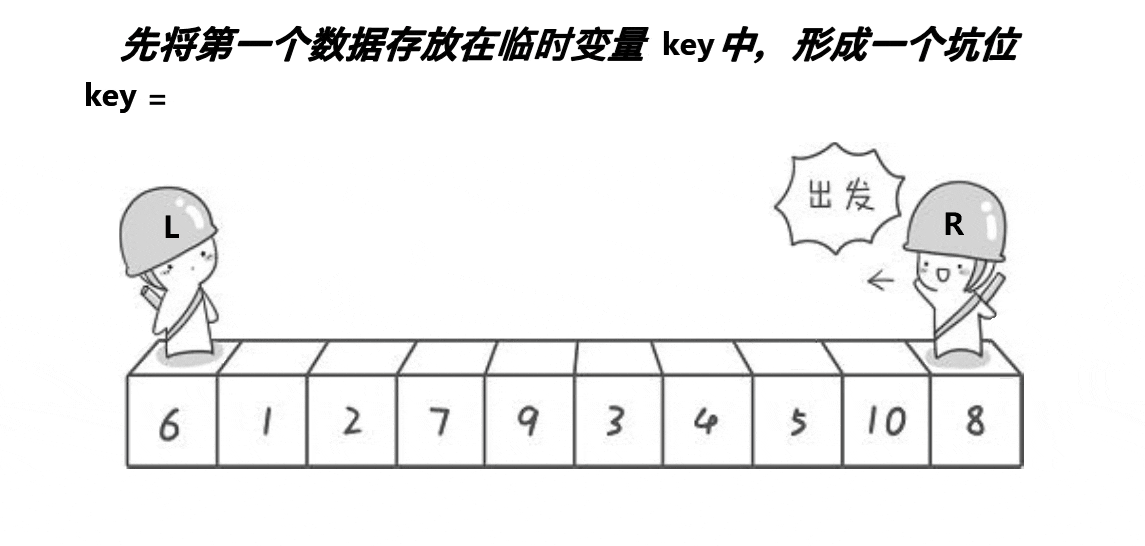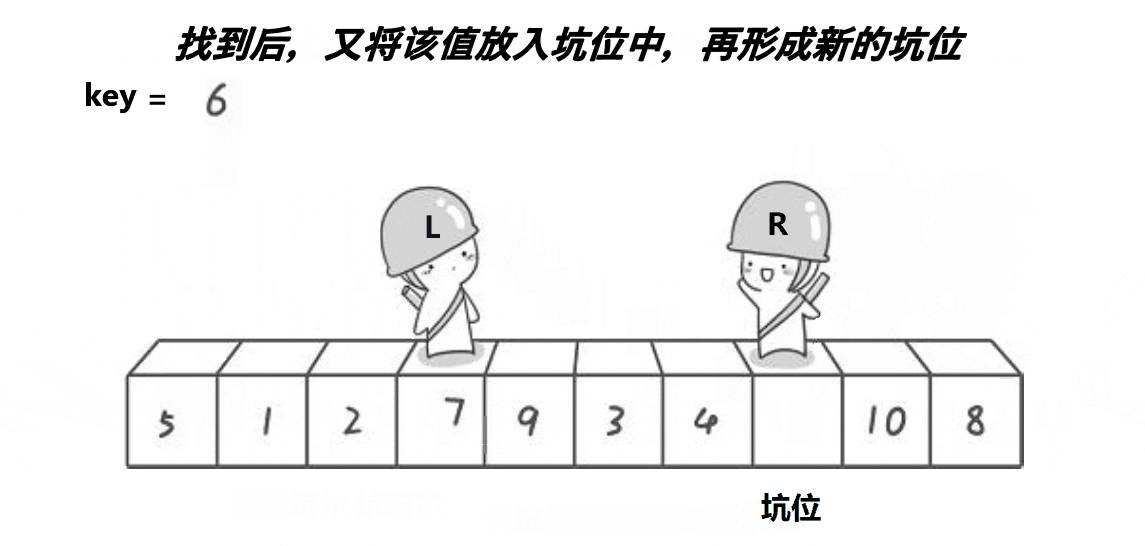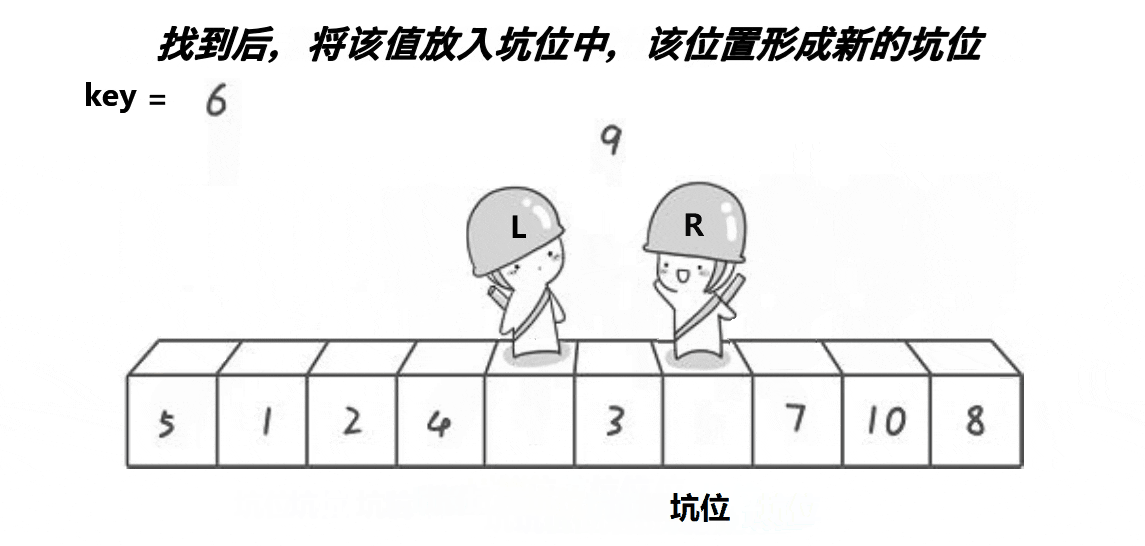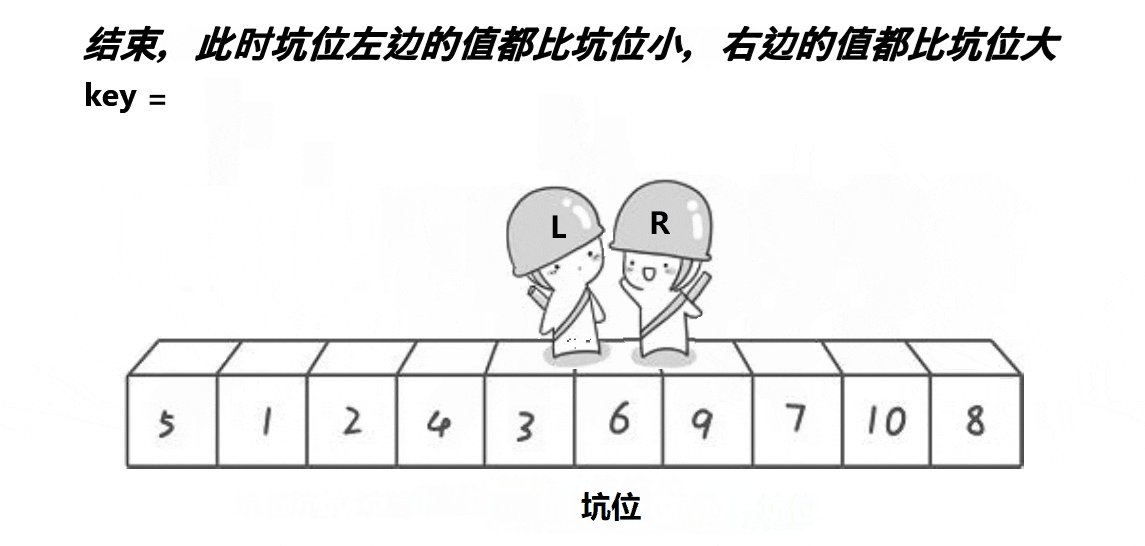
  其主要思想为：

• 创建四个变量：hole  key begin  end 
• hole为坑位，key等于数组首元素的值，先将key处的数值拿走，hole即在key处为坑位，end从右边开始找比key小的值，begin从左边开始找比key大的值。
• end找到比key晓得值以后，将end的值放到hole处，然后end处就变成了新的坑位，再让begin找大，找到以后再将值放到坑位处，begin处形成新的坑位。依次循环遍历数组
• 当begin和end相遇后就把key的值放到坑位。
• 将交换后的key的位置记录下来作为新的分割点， 再以相同的方法递归key左边和右边的元素
  
  

  完整代码展示：

void QuickSort(int* arr, int left, int right)
{
	if (left >= right)
		return;

	int key = arr[left];
	int begin = left;
	int end = right;
	int hole = begin;
	while (begin < end)
	{
		while (begin < end && arr[end] >= key)
		{
			end--;
		}
		arr[hole] = arr[end];
		hole = end;

		while (begin < end && arr[begin] <= key)
		{
			begin++;
		}
		arr[hole] = arr[begin];
		hole = begin;
	}
	arr[hole] = key;
	hole = begin;

	QuickSort(arr, left, key - 1);
	QuickSort(arr, key + 1, right);
}

三、非递归方法实现快速排序

  该方法要运用到栈的实现： 栈的实现
  用栈的实现来模拟递归从而实现快速排序。

  其主要思想为：

• 定义两个变量：left right;
• 因为栈有先进后出的特点，所以数组元素入栈时要先入尾在入头。
• 现将left和right入栈，然后再找key，这里找key可以调用前面的hoare/双指针/挖坑法的任意一个
• 再将key位置的右左两边的数入栈。

  完整代码展示：

//快速排序非递归
void QuickSortNonR(int* arr, int left, int right)
{
	ST st;
	STInit(&st);
	STPush(&st, right);
	STPush(&st, left);
	while (!STEmpty(&st))
	{
		int begin = STTop(&st);
		STPop(&st);

		int end = STTop(&st);
		STPop(&st);

		int key = PartSort2(arr, begin, end);
		//begin key-1  key  key+1  end
		if (end > key + 1)
		{
			STPush(&st, end);
			STPush(&st, key + 1);
		}

		if (key - 1 > begin)
		{
			STPush(&st, key - 1);
			STPush(&st, begin);
		}
	}
	STDestroy(&st);
}

四、快速排序的优化

  此优化可适用于任意方法的可快速排序。

  在日常生活中，我们所使用排序功能的目标对象可能不会想日常练习中那样少，或许是一个非常庞大的数量，且其所提供的数据可能在原本基础上就有部分有序化，例如所给的大量数据中第一位为最小值或最大值，而这样的数据我们从一开始就进行快速排序的话，会让end从末尾一直遍历到数据首部或begin从数据首部一直遍历到末尾，拥有时间复杂度上的浪费，所以我们提出了一个 三数取中的方法来进行优化，且针对于大量数据，当所处理数据的子数据数量过少时，我们还是用快速排序的方法有点大材小用了，故针对于此我们也提出了 小区间优化的方法应对。

1、三数区中

  针对于所给目标数组第一位即为最小值或最大值而导致的时间复杂度浪费，我们可以取其数组首位，中位，末位三个数进行比较，选取其中处于中间位置的数，令其与数据首位进行交换。

• 其代码如下所示：

int GetMid(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[left] > a[mid])
	{
		if (a[mid] > a[right])
			return mid;
		else if (a[right] > a[left])
			return left;
		else
			return right;
	}
	else
	{
		if (a[mid] < a[right])
			return mid;
		else if (a[right] < a[left])
			return left;
		else
			return right;
	}
}

2、小区间优化

  对于根据分界点所得到的新子数组，若其数据量较小，我们还是用快速排序的化有些大材小用，故当数据量较小时，我们一般使用其他排序方法，如冒泡排序或插入排序等，进行快速的排序。

• 其代码如下所示：

//插入排序
void InSertSort(int* arr, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tem = arr[end + 1];
		while (end >= 0)
		{
			if (arr[end] >= tem)
			{
				arr[end + 1] = arr[end];
				end--;
			}
			else
			{
				break;
			}
		}
		arr[end + 1] = tem;
	}
}

if ((right - left + 1) < 10)
	{
		InSertSort(arr + left, right - left + 1);
	}

快速排序的优化结束，其完整代码如下所示（前后指针法快速排序）：

void Swap(int* a, int* b)
{
	int ret = *a;
	*a = *b;
	*b = ret;
}

//快速排序  hoare
void QuickSort(int* arr, int left, int right)
{
	if (left >= right)
		return;

	//小区间优化
	if (right - left < 10)
	{
		InSertSort(a, right - left + 1);
	}	

	//三数取中
	int mid = GetMid(a, left, right);
	Swap(&a[left], &a[mid]);

	int key = left;
	int begin = left;
	int end = right;

	while (begin < end)
	{
		while (begin < end && arr[end] >= arr[key])
		{
			end--;
		}
		while (begin < end && arr[begin] <= arr[key])
		{
			begin++;
		}
		Swap(&arr[begin], &arr[end]);
	}
	Swap(&arr[begin], &arr[key]);
	key = begin;

	QuickSort(arr, left, key - 1);
	QuickSort(arr, key + 1, right);
}

五、快速排序的特性总结

  快速排序的特性总结：

1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(logN)
4. 稳定性：不稳定