【matlab 代码的python复现】 Matlab实现的滤波器设计实现与Python 的库函数相同实现Scipy

一 实现一个IIR滤波器的设计

背景

Matlab 设计的滤波器通常封装过于完整，虽然在DSP中能够实现更多功能的滤波器设计但是很难实现Python端口的实现。
我们以一段原始的生物电信号EEG信号进行处理。

EEG信号

1.信号获取

EEG信号通常通过头皮电极，经过多通道采样芯片采样，将获取到的微弱的头皮模拟电信号，转化为数字信号。获取到的数字信号在处理，通常需要数字信号处理技术与脑机接口技术。例如，滤波、通道选择、频谱分析等。我们通过电极帽获取到的数字信号，按照电路的放大比例进行的放大。因此获取到的信号可能是存在基线漂移的信号，或者非零点的信号。这些都是相对于设备采集来说的。但是信号中存在的特征往往存在是主要的。我们复现Matlab的高质量设计的滤波器，python实现更有助于工程实现。

2.Matlab滤波器设计函数

打开Matlab的信号分析器。这是一个功能强大的信号可视化APP,可以完成简单的信号的预处理的工作。

导入的是一个1000个采样点的EEg原始信号，这个原始信号设置采样频率为250Hz。经过分析我们得到该信号幅值位于-900,并非处于基线附近因此我们认识到，这个信号存在基线漂移问题。我们打算通过高通或者带通滤波器实现解决。

1点击显示按钮中的频谱和时频率图像，有助于我们直接观察信号的原始成分。

频谱显示的是功率谱图像，区别是频谱图他更加的光滑。具体区别见这里功率谱，功率、功率密度http://t.csdnimg.cn/Qzldh。

能看到低频能量特别高，还有50Hz、100Hz的中间的工频噪声，以及高频噪声。

2点击分析器，设置带通滤波器

3设置滤波范围6，48Hz

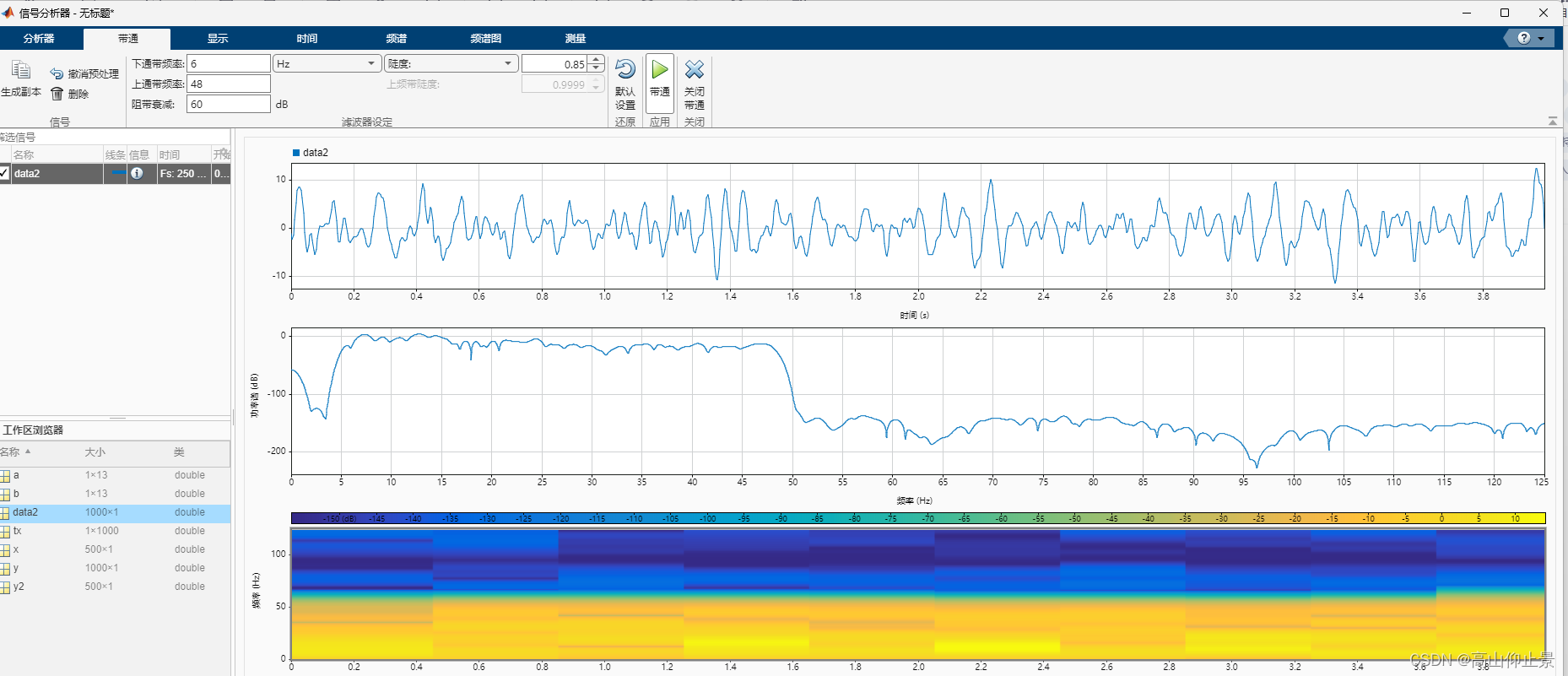
此时此刻我们观察到这个波形是去除基线漂移并且能过去除高频的波形。位于0基线附近。

点击分析器生成函数，matlab 在工作台生成一个预处理的函数。

data =load("output.mat")
data2 =squeeze(data.data(1,1,1,:));

% 定义采样频率 (Hz)
fs = 250;

% 定义采样点数
num_samples = 1000;

% 计算采样周期 (seconds)
Ts = 1/fs;

% 创建时间向量tx，范围从0到( num_samples - 1 ) * Ts
tx = (0 : num_samples - 1) * Ts;
y = preprocess(data2,tx);
plot(y)
hold on
plot(data2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

运行结果显示出来/
这是一个我认为完美的信号。

通过了解Matlab使用的是IIR auto设计的滤波系数。因此我尝试用Python实现。

3 基于Python 的Scipy.io实现滤波

def preprocess_input(x, tx):
    """
    预处理输入信号 x，根据时间向量 tx 进行带通滤波。

    参数:
        x (array_like): 输入信号数据.
        tx (array_like): 时间向量（单位：秒）.

    返回:
        array_like: 经过带通滤波处理后的信号数据.
    """
    # 计算平均采样率
    import numpy as np
    from scipy.signal import ellip, butter, lfilter, freqz, iirdesign, cheby2, buttord, cheb2ord

    Wpass1, Wpass2 = (0.0480, 0.3840)
    Wstop1, Wstop2 = (0.0405, 0.3915)
    Apass, Astop = 0.1, 60

    b, a = iirdesign(wp=[Wpass1, Wpass2], ws=[Wstop1, Wstop2],
                     gpass=Apass, gstop=Astop,
                     analog=False, ftype='elliptic')
    # 设计滤波器
    y = filtfilt(b, a, x)

    return y


# 示例使用参数
import numpy as np
data =np.load(r"2024-04-09 14_36_5_eegdata.npy")
print(data.shape)
sampling_rate = 1000.0  # 假设采样率为1000 Hz
signal =data[0,0,0,:]
time_vector = np.linspace(0, 4, 1000, endpoint=False)  # 示例时间向量
filtered_signal = preprocess_input(signal, time_vector)

#将原始信号与滤波后的信号画图
import matplotlib.pyplot as plt
plt.plot(signal, label='Original Signal')
plt.plot(filtered_signal, label='Filtered Signal')
plt.legend()
plt.show()
# 现在 `filtered_signal` 是经过带通滤波处理后的信号数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

画出的结果是这样的。

为什么使用了相同的参数输出的结果为什么和matlab差别如此之大？
为什么会出现初始的信号的阶跃震荡？
Matlab自动实现的去除基线漂移的效果为什么Python不能是实现？

4.问题分析

我们使用Matlab设计零相位滤波器带通滤波器

load noisysignals x;                    % noisy waveform
x=x-500;
[b,a] = butter(1,[24/1000,48/250],'bandpass');           % IIR filter design
y = filtfilt(b,a,x);                    % zero-phase filtering
y2 = filter(b,a,x);                     % conventional filtering
plot(x,'k-.'); grid on ; hold on
plot([y y2],'LineWidth',1.5);
legend('Noisy ECG','Zero-phase Filtering','Conventional Filtering');
figure 
plot(x)
figure
plot(y)
1
2
3
4
5
6
7
8
9
10
11
12

发现matlab归一化设计的1阶的零相位滤波器filtfile归一化频率 6/250，48/250的真的效果比较好。但是卷积filter过程似乎没有很好。为什么零相位滤波器能实现去漂移呢？
再次改变其滤波器阶数（6阶），依旧无法改变卷积filter的震荡情况。

filtfilt和filter都是Python中用于数字信号处理的函数，分别位于scipy.signal模块中。

它们的主要区别在于对信号进行滤波时处理相位的方式：
1 filter: 实施的是传统的前向-后向滤波（或称为一阶递归滤波）。它直接将输入信号通过指定的数字滤波器（如IIR或FIR滤波器），得到输出信号。这种操作通常会导致滤波后的信号产生相位延迟，即存在非零相位。
2 filtfilt: 则执行双线性递归滤波（zero-phase filtering），实质上是对信号先向前滤波一次，再向后滤波一次（或者反过来），以消除滤波过程中的相位延迟，实现零相位滤波。这样做虽然保留了原始信号的相位特性，但可能会引入一些额外的“初始跳动”现象。

初始跳动现象的原因
在处理有基线漂移的信号（如一段整体平均值为-500的信号）时，使用filtfilt和filter可能会出现初始跳动情况，原因如下：
边界效应：由于滤波器本质上是一种基于过去和当前数据计算未来输出的过程，因此在信号开始和结束处，有效历史数据不足，导致滤波器输出受到边界条件的影响。特别是在filtfilt进行前后两次滤波时，这种影响可能更为明显。初始跳动通常是边界效应造成的暂时性不稳定性。
滤波器冲击响应：滤波器的冲击响应是指当输入为单位脉冲时，滤波器的输出随时间变化的曲线。某些滤波器（尤其是IIR滤波器）的冲击响应可能包含较大的初始值，这些初始值在处理实际信号时会表现为“跳动”。filtfilt虽然消除了相位延迟，但无法改变滤波器本身的冲击响应特性，因此可能出现初始跳动。
基线漂移处理：对于有基线漂移的信号，滤波器可能特别敏感于信号的起始部分，因为这部分包含了确定基线水平的重要信息。如果滤波器设计不当或者参数选择不合适（如截止频率过低、过渡带过窄等），可能会过度平滑初始部分，导致基线偏离期望值，形成“跳动”。
解决策略
1针对上述原因，可以采取以下措施来缓解或避免初始跳动问题：
2适当预处理：在应用滤波器之前，对原始信号进行预处理，如减去平均值、平滑起始段等，以减少边界效应的影响。
3调整滤波器参数：确保滤波器的设计（如类型、阶数、截止频率、滚降率等）与信号特性和处理需求相符。对于基线漂移的信号，可能需4要选择具有较宽过渡带和平缓冲击响应的滤波器。
5使用特殊边界处理方法：filtfilt支持传递额外的参数padtype和padlen来指定边界填充方式和长度。合理选择填充方式（如’constant’、‘linear_ramp’、'mean’等）和长度可以减轻边界效应，从而改善初始跳动问题。
6考虑其他滤波技术：如果零相位滤波不是必须的，可以尝试使用filter并接受一定的相位延迟，同时适当调整滤波器参数以降低初始跳动。另外，还可以考虑使用专门针对基线漂移校正的技术，如高斯拟合、指数平滑等。

在filtfilt.m这个函数中，边缘外推（edge extrapolation）技术用于处理输入数据序列的开始和结束部分，以减少滤波过程中的启动和结束瞬态。具体实现体现在以下几个部分：

function yout = ffOneChanCat(b,a,y,zi,nfact,L)

coder.varsize('yout');
yout = y;
for ii=1:L
    % Single channel, data explicitly concatenated into one vector
    ytemp = [2*yout(1,1)-yout(nfact(1,1)+1:-1:2,1); yout(:,1); 2*yout(end,1)-yout(end-1:-1:end-nfact(1,1),1)];
    
    % filter, reverse data, filter again, and reverse data again
    ytemp = filter(b(:,ii),a(:,ii),ytemp(:,1),zi(:,ii)*ytemp(1,1),1);
    ytemp = ytemp(end:-1:1,1);
    ytemp = filter(b(:,ii),a(:,ii),ytemp(:,1),zi(:,ii)*ytemp(1,1),1);
    
    % retain reversed central section of y
    yout = ytemp(end-nfact(1,1):-1:nfact(1,1)+1,1);
    yout
end

end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

1函数 ffOneChanCat： 在该函数中，对单通道输入数据y进行边缘外推处理，以减少滤波时的边缘效应。关键代码如下：

   ytemp = [2*yout(1,1)-yout(nfact(1,1)+1:-1:2,1); yout(:,1); 2*yout(end,1)-yout(end-1:-1:end-nfact(1,1),1)];
   
1
2

这段代码首先计算了输入数据的前nfact(1,1)个样本点的线性外推值，通过减去倒数第二个到倒数第nfact(1,1)+1个样本之间的差值并乘以2，然后加上第一个样本值。同样地，对输入数据的末尾部分也进行了类似的线性外推。这样，得到的ytemp序列在开始和结束部分都包含了经过外推的数据。
2函数 ffOneChan： 对于单通道输入数据xc，边缘外推处理也在该函数中进行。关键代码如下：

%--------------------------------------------------------------------------
function y = ffOneChan(b,a,xc,zi,nfact,L)
    % Perform filtering of input data with no phase distortion
    %
    % xc: one column of input data
    % yc: one column of output, same dimensions as xc
    % a,b: IIR coefficients, both of same order/length
    % zi: initial states
    % nfact: scalar
    % L: scalar
    
    % Extrapolate beginning and end of data sequence using reflection.
    % Slopes of original and extrapolated sequences match at end points,
    % reducing transients.
    %
    % yc is length numel(x)+2*nfact
    %
    % We wish to filter the appended sequence:
    % yc = [2*xc(1)-xc(nfact+1:-1:2); xc; 2*xc(end)-xc(end-1:-1:end-nfact)];
    %
    % We would use the following code:
    % Filter the input forwards then again in the backwards direction
    %   yc = filter(b,a,yc,zi*yc(1));
    %   yc = yc(length(yc):-1:1); % reverse the sequence
    %
    % Instead of reallocating and copying, just do filtering in pieces
    % Filter the first part, then xc, then the last part
    % Retain each piece, feeding final states as next initial states
    % Output is yc = [yc1 yc2 yc3]
    %
    % yc2 can be long (matching user input length)
    % yc3 is short (nfilt samples)
    %
    for ii=1:L
        
        xt = -xc(nfact(1,1)+1:-1:2,1) + 2*xc(1,1);
        [~,zo] = filter(b(:,ii),a(:,ii), xt(:,1), zi(:,ii)*xt(1),1); % yc1 not needed
        [yc2,zo] = filter(b(:,ii),a(:,ii), xc(:,1), zo,1);
        xt = -xc(end-1:-1:end-nfact(1,1),1) + 2*xc(end,1);
        yc3 = filter(b(:,ii),a(:,ii), xt(:,1), zo,1);
        
        % Reverse the sequence
        %   yc = [flipud(yc3) flipud(yc2) flipud(yc1)]
        % which we can do as
        %   yc = [yc3(end:-1:1); yc2(end:-1:1); yc1(end:-1:1)];
        %
        % But we don't do that explicitly.  Instead, we wish to filter this
        % reversed result as in:
        %   yc = filter(b,a,yc,zi*yc(1));
        % where yc(1) is now the last sample of the (unreversed) yc3
        %
        % Once again, we do this in pieces:
        [~,zo] = filter(b(:,ii),a(:,ii), yc3(end:-1:1,1), zi(:,ii)*yc3(end,1),1);
        yc5 = filter(b(:,ii),a(:,ii), yc2(end:-1:1,1), zo,1);
        
        % Conceptually restore the sequence by reversing the last pieces
        %    yc = yc(length(yc):-1:1); % restore the sequence
        % which is done by
        %    yc = [yc6(end:-1:1); yc5(end:-1:1); yc4(end:-1:1)];
        %
        % However, we only need to retain the reversed central samples of filtered
        % output for the final result:
        %    y = yc(nfact+1:end-nfact);
        %
        % which is the reversed yc5 piece only.
        %
        % This means we don't need yc4 or yc6.  We need to compute yc4 only because
        % the final states are needed for yc5 computation.  However, we can omit
        % yc6 entirely in the above filtering step.
        xc = yc5(end:-1:1,1);
    end
    y = xc;
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

   xt = -xc(nfact(1,1)+1:-1:2,1) + 2*xc(1,1);
1

和ffOneChanCat类似，此处计算的是输入数据开始部分的线性外推值，通过对倒数第二个到倒数第nfact(1,1)+1个样本求和、乘以-1，然后加上第一个样本值的两倍。在后续代码中，xt被用于向前滤波的初始部分。
同理，对于输入数据的结束部分，也有相似的边缘外推处理：

   xt = -xc(end-1:-1:end-nfact(1,1),1) + 2*xc(end,1);
1

5 解决基线漂移的常用的方法

1信号的基线漂移是指在长时间记录过程中，信号的直流偏移或低频波动发生变化，导致信号的平均值或基准水平发生缓慢、持续的移动。这种现象在心电信号（ECG）、脑电图（EEG）、生物电信号、化学传感器输出等众多领域普遍存在，如果不加以矫正，可能会影响信号的准确解读和后续分析。以下是一些常用的基线漂移矫正方法：
a高通滤波： 应用一个合适的高通滤波器（如 Butterworth、Chebyshev、Elliptic 等）去除信号中的低频成分。通过设定截止频率，可以保留感兴趣的高频信号特征，同时滤掉导致基线漂移的低频趋势。在MATLAB中，可以使用butter、cheby2等函数设计滤波器，并使用filtfilt、lfilter等函数进行滤波,这个方法可能需要考虑是否使用延迟初始值避免震荡。
b中值滤波： 利用滑动窗口内的信号中值代替每个点的值，以减少基线漂移和噪声的影响。这种方法尤其适用于含有尖峰噪声但仍希望保持信号边缘细节的情况。在Python中，可以使用numpy库的median_filter函数实现。
c均值移除： 计算整个信号或信号段的平均值，并将其从原始信号中减去，以消除全局基线漂移。如果漂移随时间变化，可以考虑分段计算均值并相应调整。
d多项式拟合： 使用多项式（如线性、二次、三次等）对信号进行拟合，提取出基线趋势，然后从原始信号中减去拟合得到的趋势线。在Python中，可以使用numpy.polyfit和numpy.polyval函数。
e基于EMD（Empirical Mode Decomposition）或小波分解的基线校正： 将信号分解为多个本征模态函数（IMFs）和一个残余项。通常，基线漂移体现在最低频的IMF或残余项中。去除或修正这部分，再重新合成信号，即可实现基线校正。可以使用PyEMD库（针对EMD）或pywt库（针对小波分析）实现。可能需要结合实际情况尝试多种方法或对其进行组合，以找到最佳的基线校正策略。在矫正过程中，需要注意保护信号中的重要特征不受损，避免过度平滑或引入新的失真。

5.1核心函数

matlab中因为需要反复对信号方向滤波，避免这个阶跃问题，源代码通过这两函数进行了时间序列外推。之后还原。外推是通过计算倒数第二个到倒数第nfact+1数，加上倒数第一个数的二倍。得到的序列。nfact=阶数*6。例如，二阶滤波，延拓两边各加12个序列点，五阶次滤波两边各个加上30个离散序列点。

y =filter(b,a,x,zi,dim)

x：输入的时间序列
b:分子的离散传递函数系数
a:分母的离散传递函数系数
zi：延迟序列
dim:维度

5.2 滤波传递函数具体使用示例

移动平均滤波器是用于对含噪数据进行平滑处理的常用方法。此示例使用 filter 函数计算沿数据向量的平均值。

创建一个由正弦曲线数据组成的 1×100 行向量，其中的正弦曲线被随机干扰所损坏。

t = linspace(-pi,pi,100);
rng default  %initialize random number generator
x = sin(t) + 0.25*rand(size(t));
1
2
3

上述就是一个移动平均函数此时，a等于1，b等于1/4,窗口大小为4.

windowSize = 5; 
b = (1/windowSize)*ones(1,windowSize);
a = 1;
1
2
3

求数据的移动平均值，并绘制其对原始数据的图。

y = filter(b,a,x);

plot(t,x)
hold on
plot(t,y)
legend('Input Data','Filtered Data')
1
2
3
4
5
6

5.3 传递函数在滤波中的概念

% Parse SOS matrix or coefficients vectors and determine initial conditions
[b2,a2,zi,nfact,L] = getCoeffsAndInitialConditions(b,a,Npts,x);
yCol = ffOneChanCat(b2,a2,xCol,zi,nfact,L);

函数getCoeffsAndInitialConditions的主要目的是为数字信号处理中的滤波操作预处理所需的系数和初始条件。具体来说，它完成了以下任务：
1解析输入参数：
**b和a：**分别表示滤波器的分子（numerator）和分母（denominator）系数，可以是表示单个传递函数的向量，或表示第二类有理多项式（Second-Order Section, SOS）滤波器的矩阵。
Npts：输入数据点数。
**x：**输入信号（未在函数内使用，可能用于外部错误检查）。
2处理SOS滤波器：
如果输入参数表示一个SOS滤波器（issos为真），函数会调整分子系数以包含缩放值（g），确保每个子系统中a0系数非零，并计算归一化后的系数b1和a1。
计算滤波器阶数（ord）和边缘过渡长度（nfact）。
根据SOS矩阵计算初始状态向量zi，以消除滤波前后信号的直流偏移。
3处理常规传递函数滤波器：
如果输入参数表示一个常规传递函数，函数会确保分母首项a(1)非零，并计算归一化后的系数b1和a1。
计算滤波器阶数对应的边缘过渡长度（nfact）。
根据传递函数系数计算初始状态向量zi，同样用于消除滤波前后信号的直流偏移。
关于变量zi：
zi是一个二维数组（列向量），代表滤波器的初始状态。在数字信号处理中，当使用递归滤波器（如IIR滤波器）时，除了当前输入样本外，滤波器的输出还依赖于其内部的“记忆”状态。这些状态在时间上累积了过去的输入信息，对于保持滤波器稳定性和保证输出质量至关重要。
在本函数中，zi的具体计算方式取决于输入参数b和a所表示的滤波器类型（SOS或常规传递函数）：
对于SOS滤波器：
对于每一个第二阶子系统（共L个），通过求解线性方程组计算出对应两个状态的初始值（即zi(:,ii)），线性方程组的系数和常数项与该子系统的归一化系数有关。
对于常规传递函数滤波器：
如果滤波器阶数大于1，利用稀疏矩阵或稠密矩阵（根据编译选项和目标平台决定）求解线性方程组，得到滤波器所有状态（阶数减1个）的初始值。
如果滤波器阶数为1，zi为空数组，因为一阶滤波器没有内部状态。
简而言之，变量zi是滤波器开始工作前需要预先设置的状态向量，它通过求解特定线性方程组得到，确保滤波过程开始时滤波器处于已知且稳定的初始状态，进而确保滤波效果的准确性和稳定性。特别是在进行filtfilt双边滤波时，正确的zi有助于消除滤波前后信号的直流偏移，确保输出信号在时间起点和终点处连续。

二 Matlab转Python 的零相位滤波器代码

1 python实现一个与matlab滤波效果一摸一样的滤波函数代码
a 采样频率250Hz，任意滤波器设计滤波函数传递函数系数a,b，无边界效应产生的震荡。
b 有滤波初始条件计算初始条件的功能的滤波函数，设计非线性延拓，这里设定为6个延拓点。
c 设定一个滤波器实现零相位正向反向滤波。
d 该滤波方法可以有效去除基线漂移
原始信号：

原始的没有进行边界效应的滤波器结果，在初始阶段产生明显的震荡：

处理之后：

3处理前后信号对比
method_pad:zero

Matlab中明显可以看到也是存在这种情况：如果从底层原理上处理的话,我们matlab仿真了这个相同的滤波效果。
这说明必要的步骤matlab集成的更加好，但是python编写的时候需要考虑。

method_pad:linear

from scipy.signal import ellip, lfilter
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import butter, lfilter_zi
def python_filtfilt(b, a, y, nfact=3, method='mirror'):
    """
    Apply forward-backward filtering with initial conditions and bilateral padding.

    Parameters:
    b (ndarray): Numerator filter coefficients.
    a (ndarray): Denominator filter coefficients.
    y (ndarray): Input signal.
    nfact (int, optional): Length of edge transients. Defaults to 3.
    method ('pad' or 'mirror'): Padding method. Defaults to 'pad'.

    Returns:
    ndarray: Filtered signal.
    """
    nfact=nfact*6
    def create_mirrored_extension(yout, nfact):
        """
        Create a mirrored extension for the given signal `yout`.

        Parameters:
        yout (ndarray): Original signal.
        nfact (int): Length of the extension.

        Returns:
        ndarray: Mirrored extension.
        """
        Npts = len(yout)
        print(Npts)

        # Left-side extension (linearly decreasing from yout[0] to yout[1])
        left_ext = np.empty(nfact)
        left_ext[0] = yout[0]
        left_ext[1:] = 2 * yout[0] - yout[2:nfact + 1]


        # Right-side extension (linearly increasing from yout[-1] to yout[-2])
        right_ext = np.empty(nfact)
        right_ext[-1] = yout[-1]
        right_ext[:-1] = 2 * yout[-1] - yout[-2: -nfact - 1:-1]


        # Concatenate the original signal with the extensions
        ytemp = np.concatenate((left_ext, yout, right_ext))
        print(ytemp.shape)

        return ytemp
    # Calculate initial conditions (zi) for lfilter
    zi = lfilter_zi(b, a)

    # Bilateral padding
    Npts = len(y)
    if method == 'pad':
        # Pad with zeros on both ends
        y_padded = np.concatenate((np.zeros(nfact), y, np.zeros(nfact)))
    elif method == 'mirror':
        # Mirror padding on both ends
        y_padded = np.concatenate((
            np.flip(2*y[1]-y[1:nfact+1], axis=0),
            y,
            np.flip(2*y[-1]-y[-nfact-2:-2], axis=0)
        ))
    elif method=="linear":
        y_padded = create_mirrored_extension(y, nfact)
    else:
        raise ValueError("Unsupported padding method. Choose 'pad' or 'mirror'.")

    # Forward and Backward filtering


    y_fwd, _ = lfilter(b, a, y_padded, zi=zi*y_padded[0])
    y_rev, _ = lfilter(b, a, y_fwd[::-1], zi=zi*y_fwd[-1])

    # Extract the central section of the filtered, reversed signal
    y_out = y_rev[-(Npts+nfact):-nfact][::-1]

    return y_out





data =np.load(r"2024-04-09 14_36_5_eegdata.npy")


signal =data[0,0,0,:]


# 现在 `filtered_signal` 是经过带通滤波处理后的信号数据

rp = 0.1 # 通带纹波（最大允许增益变化），一般取较小值如 0.1 或 1.0
rs = 80  # 阻带衰减（最小衰减量，以dB为单位），根据需要选择足够大的值以保证抑制效果
# 定义滤波器参数
fs = 250  # 采样率 (Hz)
lowcut = 6  # 通带下限 (Hz)
highcut = 48  # 通带上限 (Hz)

# 设计Butterworth带通滤波器
order =5  # 滤波器阶数，可以根据实际需求调整
nyq_freq = 0.5 * fs  # Nyquist frequency
low = lowcut / nyq_freq
high = highcut / nyq_freq
b, a = butter(order, [low, high], btype='band')
y_filtered = python_filtfilt(b, a, signal, nfact=6, method='linear')
#将原始信号与滤波后的信号画图
#
plt.title("order:5 bandpassfilter:6-48")
plt.plot(signal, label='Original Signal')
plt.plot(y_filtered , label='y_filtered')

plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116

三 总结

使用Python filtfilt函数无法实现设定初始条件，以及信号处理的周期延拓问题。通过设计的函数，设定延迟ZI以及延拓条件，能够完全复现matlab的信号效果。
有利于减少信号处理多余的计算，有利于减少步骤，该算法有利于工程复现。