337. 打家劫舍 III

337. 打家劫舍 III

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

示例 1:

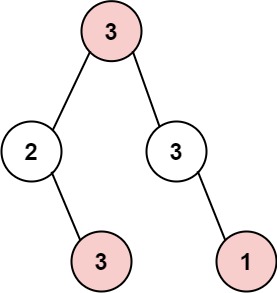
输入: root = [3,2,3,null,3,null,1]
输出: 7 
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

示例 2:

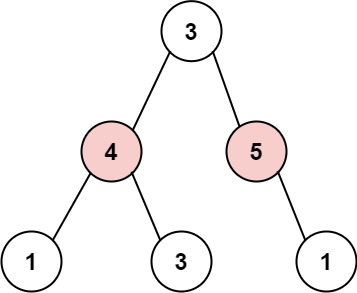
输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9

提示：

• 树的节点数在 [1, 104] 范围内
• 0 <= Node.val <= 104

    // 打家劫舍3
    public int rob(TreeNode root) {
        // 这里res就是dp
        int[] res = dfs(root);
        return Math.max(res[0], res[1]);
    }
 
    private int[] dfs(TreeNode root) {
        //    特殊值判断
        if (root == null) {
            return new int[]{0, 0};
        }
 
        // 树的后序遍历
        int[] left = dfs(root.left);
        int[] right = dfs(root.right);
 
        // dp[0]：以当前 node 为根结点的子树能够偷取的最大价值，规定 node 结点不偷
        // dp[1]：以当前 node 为根结点的子树能够偷取的最大价值，规定 node 结点偷
        int[] dp = new int[2];
 
        // 当前结点不偷： 那么就考虑左子树和右子树的子孩子偷与不偷的最大值
        dp[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        // 偷当前根结点： 那么就考虑根结点孩子的孩子的最大值，再加上当前结点
        dp[1] = root.val + left[0] + right[0];
 
        return dp;
    }