-
【leetcode】记忆化搜索
一、斐波那契数
1、题目描述
2、代码
常规递归暴搜代码:
class Solution { public: int fib(int n) { if(n == 0) return 0; if(n == 1) return 1; return fib(n - 1) + fib(n - 2); } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
备忘录版:
class Solution { public: // 备忘录 int memo[31]; int fib(int n) { memset(memo, -1, sizeof(memo)); // 先将备忘录进行初始化为-1,因为-1根本就不会遇到 return dfs(n); } int dfs(int n) { // 先判断一下在不在备忘录中 if(memo[n] != -1) // 在备忘录中就用备忘录中的 { return memo[n]; } if(n == 0 || n == 1) { memo[n] = n; return n; } memo[n] = dfs(n - 1) + dfs(n - 2); // 返回之前先保存一下 return memo[n]; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
动态规划版本:
class Solution { public: // dp表 int dp[31]; int fib(int n) { dp[0] = 0; dp[1] = 1; for(int i = 2; i <= n; i++) { dp[i] = dp[i - 1] + dp[i - 2]; } return dp[n]; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
3、解析

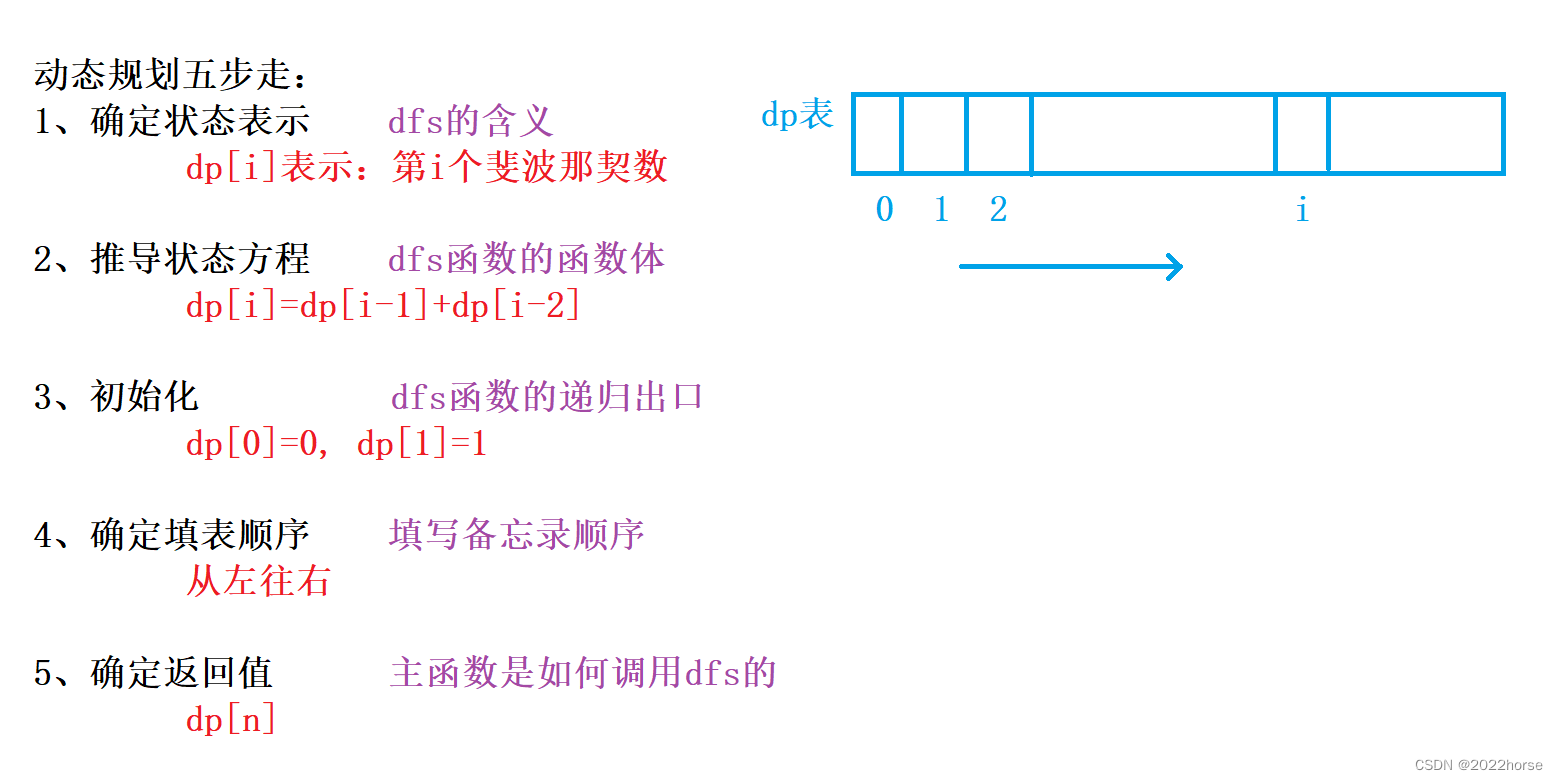

二、不同路径
1、题目描述

2、代码
记忆化搜索:
class Solution { public: vector<vector<int>> memo; int uniquePaths(int m, int n) { memo = vector<vector<int>>(m + 1, vector<int>(n + 1)); return dfs(m, n); } int dfs(int i, int j) { if(memo[i][j] != 0) { return memo[i][j]; } if(i == 0 || j == 0) { return 0; // 越界情况 } if(i == 1 && j == 1) { memo[i][j] = 1; return 1; } memo[i][j] = dfs(i - 1, j) + dfs(i, j - 1); return memo[i][j]; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
动态规划:
class Solution { public: int uniquePaths(int m, int n) { vector<vector<int>> dp(m + 1, vector<int>(n + 1)); dp[1][1] = 1; for(int i = 1; i <= m; i++) { for(int j = 1; j <= n; j++) { if(i == 1 && j == 1) { continue; } dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; } } return dp[m][n]; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
3、解析

三、最长递增子序列
1、题目描述

2、代码
记忆化搜索:
class Solution { public: int lengthOfLIS(vector<int>& nums) { int n = nums.size(); vector<int> memo(n); // 定义一个备忘录 int ret = 0; for(int i = 0; i < n; i++) { ret = max(ret, dfs(i, nums, memo)); // 相信dfs一定能处理好往后进行遍历 } return ret; } int dfs(int pos, vector<int>& nums, vector<int>& memo) { if(memo[pos] != 0) // 此处是已经使用过了 { return memo[pos]; } int ret = 1; // 必须从1开始,不然一直是0比较,会出现边界情况 for(int i = pos + 1; i < nums.size(); i++) { if(nums[i] > nums[pos]) ret = max(ret, dfs(i, nums, memo) + 1); } memo[pos] = ret; // 保存一下 return memo[pos]; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
动态规划做法:
class Solution { public: int lengthOfLIS(vector<int>& nums) { int n = nums.size(); vector<int> dp(n, 1); // 定义一个有n个数为1的dp数组 int ret = 0; // 从后往前遍历 for(int i = n - 1; i >= 0; i--) { for(int j = i + 1; j < n; j++) { if(nums[j] > nums[i]) { dp[i] = max(dp[i], dp[j] + 1); } } ret = max(ret, dp[i]); // 每次更新一下 } return ret; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
3、解析

四、猜数字大小II
1、题目描述
2、代码
class Solution { public: // 定义一个备忘录 vector<vector<int>> memo; int getMoneyAmount(int n) { memo = vector<vector<int>>(n + 1, vector<int>(n + 1)); // 暴搜 return dfs(1, n); // 传一个区间 } int dfs(int left, int right) { if(left >= right) return 0; if(memo[left][right] != 0) { return memo[left][right]; } int ret = INT_MAX; for(int head = left; head <= right; head++) { int x = dfs(left, head - 1); // 左边递归一下 int y = dfs(head + 1, right); // 右边递归一下 ret = min(ret, head + max(x, y)/*右边或者左边传上来的最大值*/); } memo[left][right] = ret; return ret; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
3、解析

五、矩阵中的最长递增路径
1、题目描述

2、代码
class Solution { public: int m, n; int dx[4] = {0, 0, 1, -1}; int dy[4] = {1, -1, 0, 0}; vector<vector<int>> memo; int longestIncreasingPath(vector<vector<int>>& matrix) { int ret = 0; m = matrix.size(); n = matrix[0].size(); memo = vector<vector<int>>(m, vector<int>(n)); for(int i = 0; i < m; i++) { for(int j = 0; j < n; j++) { ret = max(ret, dfs(matrix, i, j)); } } return ret; } int dfs(vector<vector<int>>& matrix, int i, int j) { if(memo[i][j] != 0) { return memo[i][j]; } int ret = 1; for(int k = 0; k < 4; k++) { int x = i + dx[k]; int y = j + dy[k]; if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j]) { ret = max(ret, dfs(matrix, x, y) + 1); } } memo[i][j] = ret; return ret; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
3、解析
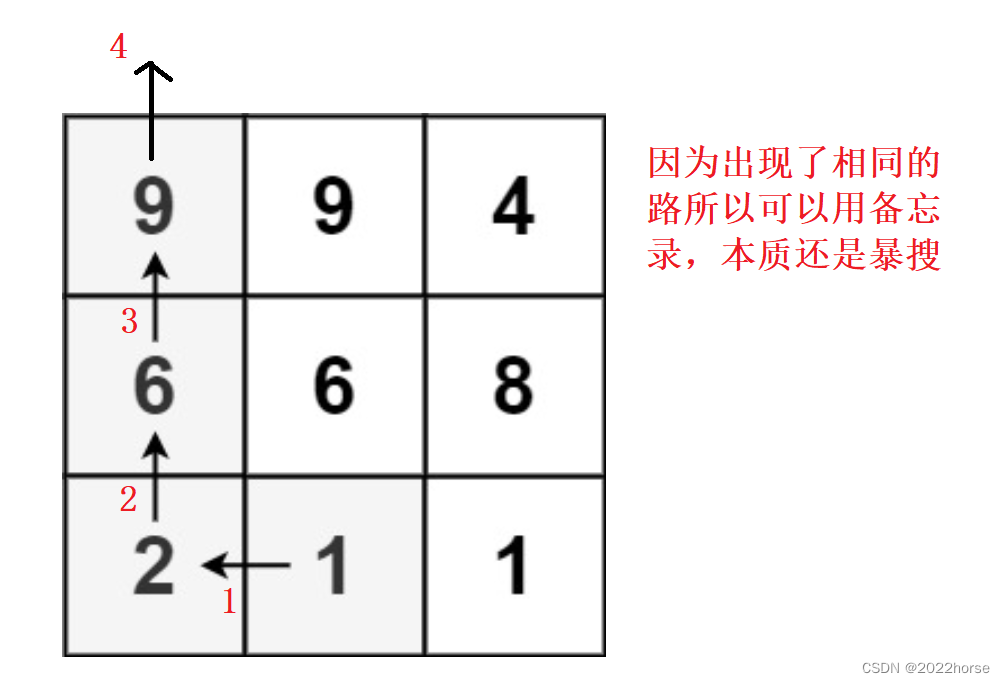
-
相关阅读:
3d激光SLAM:LIO-SAM框架---IMU预积分功能数据初始化
MySQL入门指南:数据库操作的基础知识
什么是抖音SEO?抖音SEO和传统SEO有什么区别
MySQL事务和索引
聊聊「画图」和工具
动态规划:0-1背包问题
初识Java 18-1 泛型
Linux学习——线程的控制
100天精通Python(数据分析篇)——第49天:初识numpy模块
LeetCode-50-Pow(x, n)
- 原文地址:https://blog.csdn.net/m0_70088010/article/details/136234110


