Unity中Shader法线贴图（下）理论篇

---

前言

这篇文章，主要解决上篇文章中对于法线贴图采样出错的Bug。

• Unity中Shader法线贴图（上）

---

一、采样出错的原因

在上篇文章中，我们对法线贴图采样使用的是世界空间下的坐标。但是，我们纹理在制作时，使用的是，切线空间下的坐标，所以会导致贴图采样出错。

---

二、切线空间是什么？

切线空间（Tangent Space），一个由顶点为原点组合而成的独立的坐标空间。

在这个坐标空间中：

• X轴代表的是 顶点的切线（Tangent）
• Y轴代表的是 顶点的副切线（BiTangent）,也有别的叫法： 副法线（BiNormal）
• Z轴代表的是 顶点的法线（Normal）

因此由切线、副切线、法线组成的矩阵也被称为 TBN 矩阵

切线空间图解：

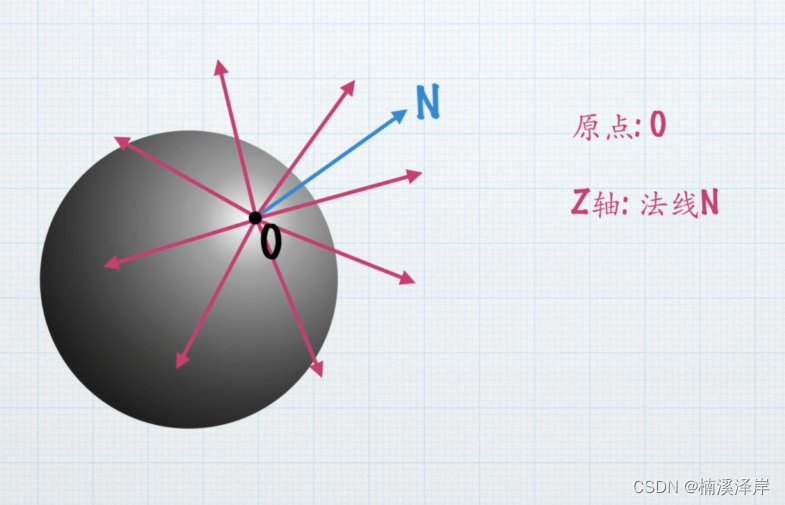
由图可得：
对于顶点来说：唯一确定的是顶点法线（z轴）。但是，和法线垂直的切线有无数条。
那么，我们需要怎么确定 哪一条切线作为 X轴（顶点切线）和 Y轴（顶点副切线）呢？
所以，我们规定
以纹理UV的 u 坐标方向为X轴（顶点切线）
以 顶点法线（Z轴） 和 顶点切线（X轴） 叉积 得出 顶点副切线（Y轴）

---

三、计算方式

计算时，必须在同一空间坐标下计算，不然会出错

1、统一变换到切线空间下进行计算

2、统一变换到世界空间下进行计算

---

四、一般统一变换到世界空间下的坐标进行计算

在上图中，在把切线空间下的法线，转化为世界空间下的法线时：
切线变换矩阵我们是已知的、切线空间下的法线我们也是已知的（法线贴图）
所以，求 世界空间下的法线时，最核心的就是求切线变换矩阵的逆矩阵M^-1。

注意：这里求的 世界空间下的法线 和之前文章中所用的不是同一个法线，之前文章中使用的法线，都是模型顶点世界空间下的法线，这里的时 法线贴图上的法线转化到世界空间后的法线。

1、求M^-1

M矩阵有着如下性质：

图中：
Tangent _x :代表切线上的单位向量的X坐标 = 1
Tangent _y :代表切线上的单位向量的Y坐标 = 0
Tangent _z :代表切线上的单位向量的Z坐标 = 0
BiTangent _x :代表副切线上的单位向量的X坐标 = 0
BiTangent _y :代表副切线上的单位向量的Y坐标 = 1
BiTangent _z :代表副切线上的单位向量的Z坐标 = 0
Normal _x :代表法线上的单位向量的X坐标 = 0
Normal _y :代表法线上的单位向量的Y坐标 = 0
Normal _z :代表法线上的单位向量的Z坐标 = 1

由此可以知道 M 是 单位矩阵，也可以得出 M 是正交矩阵，得出 M^t = M^-1。

2、求出n_w