数据结构与算法-生成树与最小生成树

🎈1.生成树与最小生成树

🔭1.1生成树与最小生成树的概念

设G=(V,E)是一个连通图，G的一个生成子图若本身是一棵树，称它为G的一棵生成树。任何连通图都有生成树。

不难看出，有n个顶点的连通图的生成树必定有n-1条边，生成树是连通图的极小子图，在生成树中任意增加一条边，必定产生回路。
✅设G=(V,E)是一个带权连通图，其生成树上任一条边e的权值称为该边的代价W(e),G的一棵生成树T的代价W（T）就是生成树中各边的代价之和。在G的所有生成树中，代价最小的生成树称为最小代价生成树，简称最小生成树。

🔭1.2最小生成树的生成准则

✅最小生成树的生成准则：

• 只能选用该图中的边来构造最小生成树。
• 必须使用且仅能使用n-1条边来连接连通图中的n个顶点。
• 选用的n-1条边不能产生回路。
• 尽量选取权值小的边。

🔭1.3两种最小生成树算法

• Kruskal算法：通常适用于稀疏图
• Prim算法：通常适用于稠密图

🏆1.3.1Kruskal算法

Kruskal算法是一种按照权值的递增次序选择合适的边来构造最小生成树的方法。

🔎设G=(V,E)是一个具有n个顶点的带权连通无向图，T=(V,TE)是G的最小生成树，则构造最小生成树的步骤如下：

1. 构造一个由n个顶点组成，不含任何边的图T=(V,∅),即TE为空集（其中每个顶点构成一个连通分量）。
2. 不断从E中取出代价最小的一条边，若该边未使T形成回路（即该边的两个顶点来自T中不同的连通分量），则将此边加入到TE中，否则舍去此边选择下一条代价最小的边。以此类推，知道TE中包含n-1条边。

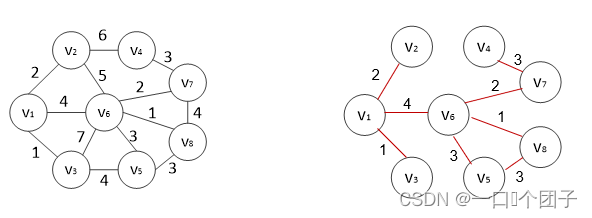
🎠Kruskal算法示例：

🏆1.3.2Prim算法

🔎设G=(V,E)是一个具有n个顶点的带权连通无向图，T=(V,TE)是G的最小生成树，则构成最小生成树的步骤如下：

1. 设置一个集合U，在图G上任选一个点u0加入U,算法从U={u0},TE=∅开始，重复执行下列操作。
2. 在所有u属于U,v属于V-U的边（u,v）中找一条代价最小的边（u0,v0）并入集合TE,同时v0并入U,直至U=V为止。此时TE中必有n-1条边，T=(V,TE)为G的最小生成树。
   🎠Prim算法示例：
   

🎈2.有向无环图及其应用

有向无环图是一个无环的有向图，简称DAG图。AOV网和AOE网是DAG图的两个典型应用。

🔭2.1AOV网与拓扑排序

在现代管理系统中，人们常用有向图来描述和分析一项工程的计划和实施过程，一个工程常被分为多个子工程，这些子工程被称为活动。在有向图中若以顶点表示活动，有向边表示活动之间的优先关系的图称为AOV网。

若（Vi,Vj）是图中的有向边，则Vi是Vj的直接前驱；Vj是Vi的直接后继。若存在一条从Vi到Vj的路径，则称Vi是Vj的前驱，Vj是Vi的后继。AOV网中不允许有回路，若存在回路，则意味着某项活动以自己为先决条件。

把AOV网络中各顶点 按照它们互相之间的优先关系排列成的一个线性序列称为一个拓扑有序序列。若Vi是Vj的前驱，则Vi一定排在Vj之前，对于没有优先关系的点，顺序任意。
在AOV网中构造一个拓扑有序序列的过程称为拓扑排序。

🏆2.1.1拓扑排序方法

🔎拓扑排序的方法：

1. 从有向图中选一个没有前驱的顶点并输出之。
2. 从图中删除该顶点和所有以它为尾的弧。
3. 重复上述两个步骤，直至全部顶点均已输出；或者当图中不存在无前驱的顶点为止（此时说明图中有环）。
   
   📝对于上图，拓扑排序的序列为：V1 V5 V4 V3 V2 V6
   注：拓扑排序的结果不一定唯一！

🏆2.1.2拓扑排序的算法流程

✅拓扑排序算法流程如下：
（1）.把邻接表中入度为0的顶点依次进栈。
（2）.若栈不空，则栈顶元素Vj退栈并输出，在邻接表中查找Vj的直接后继Vk,把Vk的入度减1；若Vk的入度为0，则进栈，继续该过程。
（3）.若顶点个数不为n（n为有向图的顶点数），则有向图有环；否则，拓扑排序完毕。

int ALGraph::TopSort()
{
	LinkStack s;
	int i, j, k;
	ArcNode* p;
	int indegree[MaxVex];
	findindegree(indegree);
	for (i = 0; i < ag, vexnum; i++)
	{
		if (indegree[i] == 0)
		{
			s.Push(i);
		}
	}
	int count = 0;
	while (!s.EmptyStack())
	{
		s.Pop(j);
		cout << ag.vertices[j].data;
		count++;
		for (p = ag.vertices[j].firstarc; p != NULL; p = p->nextarc)
		{
			k = p->adjvex;
			indegree[k]--;
			if (indegree[k] == 0)
				s.Push(k);
		}
	}
	if (count < ag.vexnum)
	{
		cout << "图中存在回路，不存在拓扑排序" << endl;
		return 0;
	}
	else
	{
		cout << "是一个拓扑排序" << endl;
		return 1;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

🔭2.2AOV网与关键路径

带权的有向无环图，称为AOE网，其中顶点表示事件，弧（有向边）表示活动，权表示活动持续时间。在工程上常用工程进度计划。通常每个工程只有一个开始事件和一个结束事件，在表示工程的AOE网中，表示整个工程的开始点（入度为0的顶点）称为源点。表示整个工程的结束点（出度为0的顶点）称为汇点。在AOE网上，从源点到汇点的路径长度最长的一条路径，或者全部由关键活动（即不按期完成就会影响整个工程完成的活动）构成的路径称为关键路径。

🏆2.2.1事件的最早发生时间（ve）

设AOE网有n个顶点，用1表示源点，n表示汇点，j表示AOE网中的第j个顶点。事件j的最早发生时间ve(j),从源点1到j结点的最长的路径，意味着事件j最早能够发生的时间，这个时间决定了所有以j为头的弧所表示的活动的最早开始时间。源点的最早发生时间为0，即ve(1)=0,从ve(1)=0开始向汇点递推，设事件j是事件i的直接后继，则ve(j)=max{ve(i)+dut(i,j)|(i,j)属于T,2<=j<=n},其中T是所有以i顶点为尾，j顶点为头的弧的集合。

若顶点旁边的值代表顶点的最早发生时间，则ve(j)=16.

🏆2.2.2事件的最迟发生时间（vl）

事件j的最迟发生时间vl(j):不影响工程的如期完成，事件j必须发生的时间。汇点的最迟发生时间vl(n)=ve(n),即汇点的最早发生时间等于最迟发生时间，从vl(n)开始向源点递推。设事件j是事件i的直接前驱，则vl(j)=min{vl(i)-dut(j,i)|(j,i)属于S，1<=j<=n-1}其中，S是所有以i为顶点，j顶点为尾的弧的集合。

图中若顶点旁边的值代表该顶点的最迟发生时间，则vl(j)=7.

🏆2.2.3例题