-
[PyTorch][chapter 61][强化学习-免模型学习 off-policy]
前言:
蒙特卡罗的学习基本流程:
Policy Evaluation : 生成动作-状态轨迹,完成价值函数的估计。
Policy Improvement: 通过价值函数估计来优化policy。
同策略(one-policy):产生 采样轨迹的策略
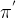 和要改善的策略
和要改善的策略 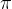 相同。
相同。Policy Evaluation : 通过
 -贪心策略(
-贪心策略(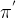 ),产生(状态-动作-奖赏)轨迹。
),产生(状态-动作-奖赏)轨迹。Policy Improvement: 原始策略也是
 -贪心策略(
-贪心策略(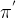 ), 通过价值函数优化,
), 通过价值函数优化,  -贪心策略(
-贪心策略(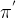 )
)异策略(off-policy):产生采样轨迹的 策略
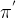 和要改善的策略
和要改善的策略 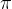 不同。
不同。Policy Evaluation : 通过
 -贪心策略(
-贪心策略(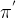 ),产生采样轨迹(状态-动作-奖赏)。
),产生采样轨迹(状态-动作-奖赏)。Policy Improvement: 改进原始策略
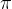
两个优势:
1: 原始策略不容易采样
2: 降低方差
易策略常用的方案为 IR(importance sample) 重要性采样
Importance sampling is a Monte Carlo method for evaluating properties of a particular distribution, while only having samples generated from a different distribution than the distribution of interest. Its introduction in statistics is generally attributed to a paper by Teun Kloek and Herman K. van Dijk in 1978,[1] but its precursors can be found in statistical physics as early as 1949.[2][3] Importance sampling is also related to umbrella sampling in computational physics. Depending on the application, the term may refer to the process of sampling from this alternative distribution, the process of inference, or both.
一 importance-samling

1.1 原理
原始问题:
u f = ∫ x p ( z ) f ( z ) d x " role="presentation" style="position: relative;">如果采样N次,得到
z 1 , z 2 , . . . z N u f ≈ 1 N ∑ z i ∼ p ( z ) f ( z i ) " role="presentation" style="position: relative;">问题:
p ( z ) " role="presentation" style="position: relative;"> 很难采样(采样空间很大,很多时候只能采样到一部分)引入 q(x) 重要性分布(这也是一个分布,容易被采样)
 : 称为importance weight
: 称为importance weight
 (大数定理)
(大数定理)下面例子,我们需要对
w ( x i ) " role="presentation" style="position: relative;">,做归一化处理,更清楚的看出来占比下面代码进行了归一化处理,方案如下:
w ( x i ) = l o g p ( x i ) − l o g q ( x i ) " role="presentation" style="position: relative;">
w 2 ( x i ) = w ( x i ) − l o g ∑ j ( e w ( x j ) ) " role="presentation" style="position: relative;">- # -*- coding: utf-8 -*-
- """
- Created on Wed Nov 8 16:38:34 2023
- @author: chengxf2
- """
- import numpy as np
- import matplotlib.pyplot as plt
- from scipy.special import logsumexp
- class pdf:
- def __call__(self,x):
- pass
- def sample(self,n):
- pass
- #正太分布的概率密度
- class Norm(pdf):
- #返回一组符合高斯分布的概率密度随机数。
- def __init__(self, mu=0, sigma=1):
- self.mu = mu
- self.sigma = sigma
- def __call__(self, x):
- #log p 功能,去掉前面常数项
- logp = (x-self.mu)**2/(2*self.sigma**2)
- return -logp
- def sample(self, N):
- #产生N 个点,这些点符合正太分布
- x = np.random.normal(self.mu, self.sigma,N)
- return x
- class Uniform(pdf):
- #均匀分布的概率密度
- def __init__(self, low, high):
- self.low = low
- self.high = high
- def __call__(self, x):
- #logq 功能
- N = len(x)
- a = np.repeat(-np.log(self.high-self.low), N)
- return -a
- def sample(self, N):
- #产生N 点,这些点符合均匀分布
- x = np.random.uniform(self.low, self.high,N)
- return x
- class ImportanceSampler:
- def __init__(self, p_dist, q_dist):
- self.p_dist = p_dist
- self.q_dist = q_dist
- def sample(self, N):
- #采样
- samples = self.q_dist.sample(N)
- weights = self.calc_weights(samples)
- normal_weights = weights - logsumexp(weights)
- return samples, normal_weights
- def calc_weights(self, samples):
- #log (p/q) =log(p)-log(q)
- return self.p_dist(samples)-self.q_dist(samples)
- if __name__ == "__main__":
- N = 10000
- p = Norm()
- q = Uniform(-10, 10)
- sampler = ImportanceSampler(p, q)
- #samples 从q(x)采样出来的点,weight_sample
- samples,weight_sample= sampler.sample(N)
- #以weight_sample的概率,从samples中抽样 N 个点
- samples = np.random.choice(samples,N, p = np.exp(weight_sample))
- plt.hist(samples, bins=100)
二 易策略 off-policy 原理

target policy
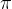 : 原始策略
: 原始策略 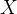 : 这里面代表基于原始策略,得到的轨迹
: 这里面代表基于原始策略,得到的轨迹[ s 0 , a 0 , r 1 , . . . . s T − 1 , a T − 1 , r T , s T ]  该轨迹的概率
该轨迹的概率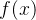 : 该轨迹的累积奖赏
: 该轨迹的累积奖赏期望的累积奖赏:

behavior policy
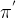 : 行为策略
: 行为策略q(x): 代表各种轨迹的采样概率
则累积奖赏函数f在概率p 也可以等价的写为:

![E[f] \approx \frac{1}{m}\sum_{i=1}^{m}\frac{p(x_i)}{q(x_i)}f(x_i)](https://1000bd.com/contentImg/2023/11/22/015531269.png)
 和
和  分别表示两个策略产生i 条轨迹的概率,对于给定的一条轨迹
分别表示两个策略产生i 条轨迹的概率,对于给定的一条轨迹[ s 0 , a 0 , r 1 , . . . . s T − 1 , a T − 1 , r T , s T ] 原始策略
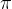 产生该轨迹的概率:
产生该轨迹的概率:

则

若
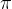 为确定性策略,但是
为确定性策略,但是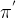 是
是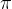 的
的 贪心策略:
贪心策略:原始策略

行为策略:

现在通过行为策略产生的轨迹度量权重w
理论上应该是连乘的,但是
 ,
,考虑到只是概率的比值,上面可以做个替换

其中:
w i = e p i e q i = e p i − q i 其核心是要计算两个概率比值,上面的例子是去log,再归一化
三 方差影响

四 代码

代码里面R的计算方式跟上面是不同的,


- # -*- coding: utf-8 -*-
- """
- Created on Wed Nov 8 11:56:26 2023
- @author: chengxf2
- """
- import numpy as ap
- # -*- coding: utf-8 -*-
- """
- Created on Fri Nov 3 09:37:32 2023
- @author: chengxf2
- """
- # -*- coding: utf-8 -*-
- """
- Created on Thu Nov 2 19:38:39 2023
- @author: cxf
- """
- import numpy as np
- import random
- from enum import Enum
- class State(Enum):
- #状态空间#
- shortWater =1 #缺水
- health = 2 #健康
- overflow = 3 #溢水
- apoptosis = 4 #凋亡
- class Action(Enum):
- #动作空间A#
- water = 1 #浇水
- noWater = 2 #不浇水
- class Env():
- def reward(self, state):
- #针对转移到新的环境奖赏
- r = -100
- if state is State.shortWater:
- r =-1
- elif state is State.health:
- r = 1
- elif state is State.overflow:
- r= -1
- else: # State.apoptosis
- r = -100
- return r
- def action(self, state, action):
- if state is State.shortWater:
- if action is Action.water :
- newState =[State.shortWater, State.health]
- p =[0.4, 0.6]
- else:
- newState =[State.shortWater, State.apoptosis]
- p =[0.4, 0.6]
- elif state is State.health:
- #健康
- if action is Action.water :
- newState =[State.health, State.overflow]
- p =[0.6, 0.4]
- else:
- newState =[State.shortWater, State.health]
- p =[0.6, 0.4]
- elif state is State.overflow:
- #溢水
- if action is Action.water :
- newState =[State.overflow, State.apoptosis]
- p =[0.6, 0.4]
- else:
- newState =[State.health, State.overflow]
- p =[0.6, 0.4]
- else:
- #凋亡
- newState=[State.apoptosis]
- p =[1.0]
- #print("\n S",S, "\t prob ",proba)
- nextState = random.choices(newState, p)[0]
- r = self.reward(nextState)
- return nextState,r
- def __init__(self):
- self.name = "环境空间"
- class Agent():
- def initPolicy(self):
- #初始化累积奖赏
- self.Q ={} #(state,action) 的累积奖赏
- self.count ={} #(state,action) 执行的次数
- for state in self.S:
- for action in self.A:
- self. Q[state, action] = 0.0
- self.count[state,action]= 0
- action = self.randomAction()
- self.policy[state]= Action.noWater #初始化都不浇水
- def randomAction(self):
- #随机策略
- action = random.choices(self.A, [0.5,0.5])[0]
- return action
- def behaviorPolicy(self):
- #使用e-贪心策略
- state = State.shortWater #从缺水开始
- env = Env()
- trajectory ={}#[s0,a0,r0]--[s1,a1,r1]--[sT-1,aT-1,rT-1]
- for t in range(self.T):
- #选择策略
- rnd = np.random.rand() #生成随机数
- if rnd <self.epsilon:
- action =self.randomAction()
- else:
- #通过原始策略选择action
- action = self.policy[state]
- newState,reward = env.action(state, action)
- trajectory[t]=[state,action,reward]
- state = newState
- return trajectory
- def calcW(self,trajectory):
- #计算权重
- q1 = 1.0-self.epsilon+self.epsilon/2.0 # a== 原始策略
- q2 = self.epsilon/2.0 # a!=原始策略
- w ={}
- for t, value in trajectory.items():
- #[state, action,reward]
- action =value[1]
- state = value[0]
- if action == self.policy[state]:
- p = 1
- q = q1
- else:
- p = 0
- q = q2
- w[t] = round(np.exp(p-q),3)
- #print("\n w ",w)
- return w
- def getReward(self,t,wDict,trajectory):
- p = 1.0
- r= 0
- #=[state,action,reward]
- for i in range(t,self.T):
- r+=trajectory[t][-1]
- w =wDict[t]
- p =p*w
- R = p*r
- m = self.T-t
- return R/m
- def improve(self):
- a = Action.noWater
- for state in self.S:
- maxR = self.Q[state, a]
- for action in self.A:
- R = self.Q[state,action]
- if R>=maxR:
- maxR = R
- self.policy[state]= action
- def learn(self):
- self.initPolicy()
- for s in range(1,self.maxIter): #采样第S 条轨迹
- #通过行为策略(e-贪心策略)产生轨迹
- trajectory =self.behaviorPolicy()
- w = self.calcW(trajectory)
- print("\n 迭代次数 %d"%s ,"\t 缺水:",self.policy[State.shortWater].name,
- "\t 健康:",self.policy[State.health].name,
- "\t 溢水:",self.policy[State.overflow].name,
- "\t 凋亡:",self.policy[State.apoptosis].name)
- #策略评估
- for t in range(self.T):
- R = self.getReward(t, w,trajectory)
- state = trajectory[t][0]
- action = trajectory[t][1]
- Q = self.Q[state,action]
- count = self.count[state, action]
- self.Q[state,action] = (Q*count+R)/(count+1)
- self.count[state, action]=count+1
- #获取权重系数
- self.improve()
- def __init__(self):
- self.S = [State.shortWater, State.health, State.overflow, State.apoptosis]
- self.A = [Action.water, Action.noWater]
- self.Q ={} #累积奖赏
- self.count ={}
- self.policy ={} #target Policy
- self.maxIter =500
- self.epsilon = 0.2
- self.T = 10
- if __name__ == "__main__":
- agent = Agent()
- agent.learn()
https://img2020.cnblogs.com/blog/1027447/202110/1027447-20211013112906490-1926128536.png
-
相关阅读:
UGUI性能优化学习笔记(二)合批
JAVA面试总结
JsJavascriptEcma的eval性能测试2208011912
【教程】Pycharm社区版中打开jupyter的方法
【Spring】事务
JetBrain Pycharm的一系列快捷键
python连接MySQL数据库服务器、使用SQL查询数据表中的所有数据
【LeetCode】Day127-四数之和 & 组合总和
衡石科技携手亚马逊云科技、浩方集团,三大势能助推出海业务数字化升级
go语言中如何实现同步操作呢
- 原文地址:https://blog.csdn.net/chengxf2/article/details/134202820
