归并排序(java)

大家好我是苏麟 , 今天说说归并排序 . 

归并排序

递归

正式学习归并排序之前，我们得先学习一下递归算法。

定义：

定义方法时，在方法内部调用方法本身，称之为递归.

public void show(){
    System.out.println("aaaa");
    show();
}

作用：

它通常把一个大型复杂的问题，层层转换为一个与原问题相似的，规模较小的问题来求解。递归策略只需要少量的 程序就可以描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。

注意事项：

在递归中，不能无限制的调用自己，必须要有边界条件，能够让递归结束，因为每一次递归调用都会在栈内存开辟 新的空间，重新执行方法，如果递归的层级太深，很容易造成栈内存溢出。

需求：

请定义一个方法，使用递归完成求N的阶乘

分析：
1!: 1
2!: 2*1=2*1!
3!: 3*2*1=3*2!
4!: 4*3*2*1=4*3!
...
n!: n*(n-1)*(n-2)...*2*1=n*(n-1)!
所以，假设有一个方法factorial(n)用来求n的阶乘，那么n的阶乘还可以表示为n*factorial(n-1)

代码实现：

public class Test {
    public static void main(String[] args) throws Exception {
        int result = factorial(5);
        System.out.println(result);
    }
    public static int factorial(int n){
        if (n==1){
            return 1;
        }
        return n*factorial(n-1);
    }
}

归并排序

归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用分治法的一个非常典型的应用。将已有序的子 序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序 表，称为二路归并。

需求：

排序前：{8,4,5,7,1,3,6,2} 排序后：{1,2,3,4,5,6,7,8}

排序原理：

1.尽可能的一组数据拆分成两个元素相等的子组，并对每一个子组继续拆分，直到拆分后的每个子组的元素个数是 1为止。

2.将相邻的两个子组进行合并成一个有序的大组；

3.不断的重复步骤2，直到最终只有一个组为止。

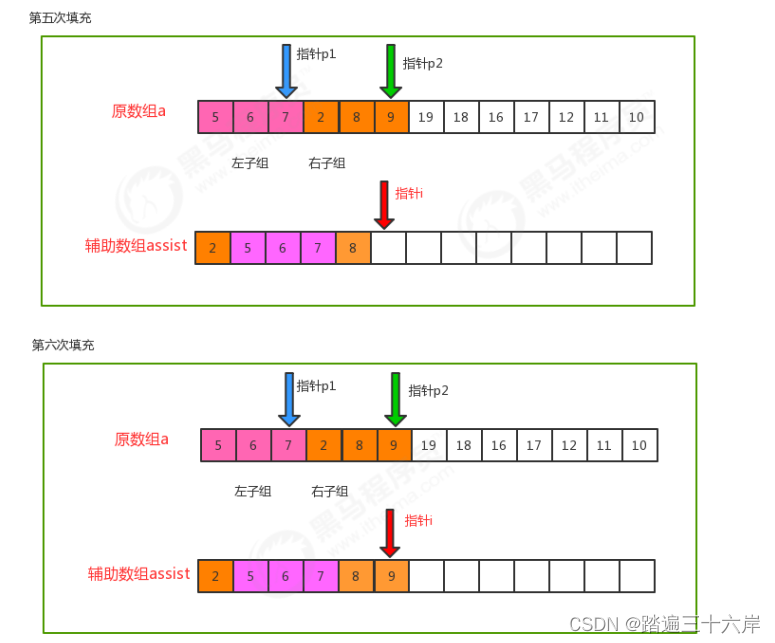
代码 :

package src.sl.sort;
 
 
/**
 * 归并排序
 * 数据类型 : int
 */
public class MergeSort {
    //辅助数组
    public static int[] assist;
 
    public static void main(String[] args) {
        int[] arr = new int[]{2,5,6,1,3,2,4,8,6,7,5};
 
        sort(arr);
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
    }
    /**
     * 对数组全部排序
     *
     * @param arr
     */
    public static void sort(int[] arr) {
 
        assist = new int[arr.length];
 
        int left = 0;
        int right = arr.length-1;
 
        sort(arr, left, right);
    }
 
    /**
     * 对数组部分排序
     *
     * @param arr
     * @param left
     * @param right
     */
    public static void sort(int[] arr, int left, int right) {
        if (left >= right) {
            return;
        }
 
        int mid = left +  (right-left) / 2;
        sort(arr, left, mid);
        sort(arr,mid + 1,right);
        //归并
        merge(arr, left, mid, right);
    }
 
 
    /**
     * 归并
     *
     * @param arr
     * @param left
     * @param mid
     * @param right
     */
    public static void merge(int[] arr, int left, int mid, int right) {
        int i = left;
        int p1 = left;
        int p2 = mid + 1;
 
        while (p1 <= mid && p2 <= right){
            if (arr[p1] < arr[p2]){
                assist[i++] = arr[p1++];
            }else {
                assist[i++] = arr[p2++];
            }
        }
 
        while (p1 <= mid){
            assist[i++] = arr[p1++];
        }
        while (p2 <= right){
            assist[i++] = arr[p2++];
        }
 
        for (int j = left; j<=right;j++){
            arr[j] = assist[j];
        }
    }
}

这期就到这里 , 下期见!