数据挖掘（5）分类数据挖掘：基于距离的分类方法

一、分类挖掘的基本流程

最常用的就是客户评估

1.1分类器概念

1.2分类方法

• 基于距离的分类方法
• 决策树分类方法
• 贝叶斯分类方法

1.3分类的基本流程

1. 步骤

   1. 建立分类模型
      • 通过分类算法对训练集训练，得到有指导的学习、有监督的学习
      • 预定义的类：类标号属性确定
   2. 使用模型进行分类
      • 测试数据集:评估模型的预测准确度
2. 流程图

3. 有指导的学习、无指导的学习

   1. 有指导学习(分类):
      • 训练样本的类标号已知。
      • 根据训练集中得到的规则对新数据进行分类
   2. 无指导学习(聚类):
      • 训练样本的类标号未知
      • 通过一系列度量等，试图确立数据中的类、聚类的存在。

1.4分类的基本问题

数据准备

评估方法

• 对用于分类、预测的方法模型进行评估
• 预测的准确率
• 速度:建立模型时间、使用模型时间
• 强壮性(鲁棒性):处理噪声和空缺值的能力
• 可伸缩(扩展性):处理大数据、构造模型能力
• 可理解性:模型的可理解能力
• 规则的优越性:判定树大小、分类规则的简洁性

二、基于距离的分类算法

1.常见的距离度量

欧几里得距离

 曼哈顿距离

 明可夫斯基距离

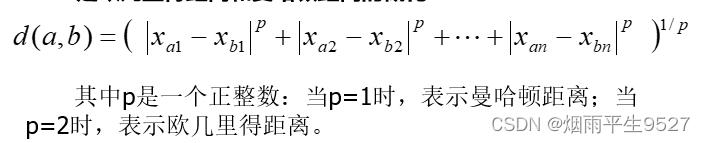
加权的明可夫斯基距离

2.K近邻分类

1. 定义:测量不同特征值之间的距离方法进行分类

2. 工作原理:

3. 优缺点

   • 优点:精度高、对异常值不敏感，无数据输入假定
   • 缺点:时空复杂度高、适用于数值型、离散型数据

4. 注意的问题

   1. K值选择：一般选择一个比较小的数，需要用大量实验来选择
   2. 结果的输出：多数表决决定
   3. 距离度量：一般采用p=2时，欧氏距离。同时注意权重问题

三、决策树分类方法

基本概念

1. 决策树：对数据进行处理、利用归纳算法生成可读的规则和决策树，并使用决策树对数据进行分类。
2. 基本组成：根节点、内部节点、叶节点
3. 两个过程
   1. 树的建立
      • 所有训练样本都在根节点
      • 根据属性来划分样本
   2. 树的剪枝
      • 许多分支可能反映的是训练数据中的噪声数据、孤立点，将这些分支剪枝
   3. 注意：
      在决策树算法中，所有属性均为符号值，即离散值，因此
      若有取连续值的属性，必须首先进行离散化。
       

决策树生成算法

1. 运用算法:贪心算法、自上而下、分治
2. 构建决策树关键:测试属性的选择
3. 注意:属性必须是离散值，在运用时要考虑是否离散化
4. 常见的决策树生成算法：CLS、ID3、C4.5、CAR

 CLS

1. 只说了划分树的方法、而没有规定选择测试属性的标准和依据
2. 选用不同属性节点会出现很大的不同
3. 举例

 ID3

1. 针对属性选择问题而提出
2. 选择最大信息增益的属性作为当前划分节点
3. 步骤:在第六章有详细说明
4. 在电信行业应用实例：
   • PPT61-70
5. 优缺点:
   • 优点：简单
   • 缺点：
     • 偏向分隔属性中取值多的一个
     • 只能处理离散属性
     • 无法对未知分隔属性处理
     • 没有剪枝操作、容易受到噪声、波动影响

C4.5

1. 在ID3算法中:偏向分割属性中取值多的一个
   • 当子集规模越小，每个子集内只有一个行，信息增益必然最大(熵最小)
   • 解决方法:增益比例
   • C4.5根据增益比例选择节点分裂属性
2. 增益比例G(X,Y)
   • 类别X、分裂属性Y
   • 
   • 引入分母H ( Y ) 偏向分割属性中取值较多的一个属性
   • 
3. 存在问题与解决的方法:

   • 取值个数过多、过少

     • 分割属性属性取值个数过多的话，H(Y)增大，但是G(X,Y)减小
     • 当取值个数很少时，存在 ，则H(Y)=0,G(X,Y)就会很大
     • 解决方法

   • ID3只能处理离散分割属性

     • ·原因:如果把连续值看做离散值，会产生分割属性偏向问题
     • 解决方法

   • 对于连续取值的属性，如何选择阈值

     • 将取值从小到大排序:{y1,y2,…,yn}
     • 对于每个yi计算增益比例，找到最大值

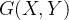
   • ID3:无法对未知分割属性进行处理

     • 原因:分割属性Y的一个取值yi,由于一些原因被计入
     • 解决方法:平均值代替(数值型属性)、概率法代替(离散属性)

   • ID3:无树剪枝，易受到噪声、波动影响

     • 解决方法:K阶交叉验证

     • 用K-1份训练决策树、用剩下的1份去测试性能，总共进行k次迭代

     • 

     • 

Cart算法(分类回归树)

1. 采用:基于最小距离的基尼指数估计函数
   • 生成二叉树
   • 可以处理连续取值的数据
     • 20、23、24、26，划分为两类一类小于某个数，另一类大于某个数
     • 但是不推荐，最好离散化
2. Gini指数
   • 
   • 

   • 取值越小，表达的不确定性越小

   • 属性必须是二叉结构

   • 计算某个属性有几个二叉结构:属性值为n,有​种划分方法

   • 举例

     •  与ID3算法一致，只是根据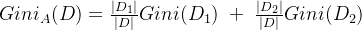计算，选择Gini指标最小的。

     • 

     • 

     • 

     • 

     • 

决策树剪枝

1. 目的:处理由于噪声数据训练出的异常，用剪枝来处理过分拟合

2. 先剪枝:

   • 在完全正确分类训练集之前就停止树的生长。
   • 最直接方法:限定树的最大生长高度,将超过树高的部分进行剪枝

3. 后剪枝:

   • "完全生长"的树剪去子树

   • 

提取分类规则

1. 从决策树的根节点到任一个叶节点所形成的一条路径构成一条分类规则。
2. 用if - then 表示

四、贝叶斯分类方法

贝叶斯推理的问题是条件概率推理问题

4.1相关概念

 举例

4.2.朴素贝叶斯分类

 

举例

 

 

 4.3朴素贝叶斯的独立假设