常见数学名词

目录

正数 positive number

负数 negative number

整数 integer number

自然数 Natural number

实数 real number

虚数 imaginary number

复数 complex number

复数的模 ∣z∣

共轭复数 conjugate complex number

复数运算法则

复数相乘的几何意义

---

正数 positive number

正数全称正实数，像+3、+1.5、+584等大于零的数，其前缀符号为“+”，可省略；

零既不是正数，也不是负数；负数与正数表示意义相反的量；

负数 negative number

负数全称负实数，像-3、-1.5、-584等小于零的数，其前缀符号为“-”；

零既不是正数，也不是负数；负数与正数表示意义相反的量；

整数 integer number

整数是正整数、0、负整数的集合，整数集使用 Z（Zahlen）表示；

整数可分为奇数和偶数；

• 奇数，不能被2整除的数；
• 偶数，能够被2整除的数；

自然数 Natural number

自然数又称非负整数，自然数集使用 N 表示；

自然数可分为偶数和奇数，合数和质数；

• 合数，是指在大于1的自然数中除了能被1和本身整除外，还能被其他数（0除外）整数的数；最小的合数为4；
• 质数，又称素数，是指在大于1的自然数中除1和本身外，不能被其他自然数整除的数；

注意，1既不是质数，也不是合数；

实数 real number

实数分有理数和无理数，实数集使用 R 表示，且实数是不可数的；

• 有理数（rational number），是整数（正整数、0、负整数）和分数的统称，是整数和分数的集合，有理数集使用 Q（Quotient）表示；有限小数及无限循环小数；
• 无理数（irrational number），无限不循环小数，不能写成两整数之比；如圆周率π、黄金比例φ，欧拉数e、开方不尽√2等；

虚数 imaginary number

形如“a+bi”、“bi”（a、b∈R，且b≠0）的复数都是虚数：

• i是虚数单位，；
• a、b均为实数；
• a为实部，b为虚部；

虚数的两种常见形式：

（1）“a+bi”（a、b∈R，并且a≠0、b≠0）；

（2）“bi”（b∈R，b≠0），也称为“纯虚数”；

复数 complex number

形如a+bi（a、b均为实数）的数为复数，复数集使用 C 表示：

Z = a + bi

• i是虚数单位，；
• a、b均为实数；
• a为实部，b为虚部；

• b=0，Z为实数；
• b≠0，Z为虚数；
• a=0，b≠0，Z为纯虚数；

复数的模 ∣z∣

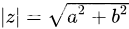
共轭复数 conjugate complex number

实部相等，虚部互为相反数的复数，互为共轭复数，记作；

 = a-bi

复数运算法则

加减法：

乘法：

除法：

复数相乘的几何意义

复数相乘 (a+bi) * (d+ei)

• 先对向量B(a,b)缩放d倍，获得向量C；
• 在对向量F(-b,a)缩放e倍（F与B垂直），获得向量H；
• 向量C与向量H相加，即得到向量G（复数相乘的结果）；

最近结果G：

• 最近结果G的幅角等于两复数幅角相加；
• 最近结果G的模长等于两复数模长的乘积；

如一个复数乘以复数，即对该复数施加旋转和拉伸（或缩放）；

在二维空间，相当于向量旋转；