笔记01：随机过程——随机游动

笔记01：随机过程——随机游动

一、伯努利随机过程

1. n次伯努利实验中（x=1）发生的总次数Yn：

$Y_n = \sum_{i=1}^{n} X_i, n=1,2,3,4,\cdots$

$P_{Y_n}(k)=\binom{n}{k}p^{k}(1-p)^{n-k}$

(二项分布)

2. 伯努利实验中事件第一次发生的时间L1：

$P_{L_1}(l)=p(1-p)^{l-1}, l=1,2,3,4,5,\cdots$

（几何分布）

3. n次伯努利实验中事件第k次发生的时间Lk：

$P_{L_k}(n) = \binom{n-1}{k-1}p^{k}(1-p)^{n-k}$

（帕斯卡分布）

二、一维随机游动

$Y_n = \sum_{k=1}^{n} X_k = Y_{n-1} + X_n$

1. 一维随机游动的位置概率

$P(Y=r)=p^{k}q^{n-k}\binom{n}{k}, k=0, 1, 2, 3, \cdots , n$

其中， $k-(n-k) = r \Rightarrow 2k-n = r \Rightarrow k=\frac{n+r}{2}$

则， $P(Y=r) = \binom{n}{\frac{n+r}{2}} p^{\frac{n+r}{2}} (1-p)^{\frac{n-r}{2}}$

其中， $r=-n,-n+2,-n+4,\cdots , n-2, n$

一维随机游动的状态转移图

赌徒输光（破产）问题

初始赌资为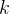元，

赌输的概率：

（1） $q \neq p$

$r_k = \frac{(q/p)^k - (q/p)^N}{1-(q/p)^N}$

（2）

$r_k = 1-\frac{k}{N}$

读赢的概率：

（1） $q \neq p$

$r_k = 1-\frac{(q/p)^k-(q/p)^N}{1-(q/p)^N} = \frac{1-(q/p)^k}{1-(q/p)^N}$

(2)

$r_k = \frac{k}{N}$

返回原点的概率

$P(Y=r) = \binom{n}{\frac{n+r}{2}} p^{\frac{n+r}{2}} (1-p)^{\frac{n-r}{2}}$

令，

$P(Y=0) =\binom{2k}{k}p^k (1-p)^k$

$u_{2n} = \binom{2n}{n}p^{n} (1-p)^{n} = \frac{(2n)!}{n! n!} (pq)^n$

$U(z) = \sum_{n} u_{2n} z^{2n} = \frac{1}{\sqrt{1-4pqz^2}}$

$\sum_{n} u_{2n} = \frac{1}{\sqrt{1-4pq}} \neq 1$

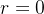第一次返回原点的概率

$B_{2n} = \left \{ Y_1 \neq 0, Y_2 \neq 0, \cdots , Y_{2n-1} \neq 0, Y_{2n} = 0 \right \}$

$v_{2n} = P(B_{2n})$

$u_{2n} = v_{2n} + u_{2}v_{2n-2} + u_{4}v_{2n-4} + \cdots + u_{2n-2}v_{2} = \sum_{k=1}^{n} v_{2k} u_{2n-2k}$
相关阅读:
【STM32】入门（六）：I2C协议
 GIS（地理信息系统/地理信息科学）怎么评职称？
前端面试基础学习笔记
 自动化测试用例的编写，只需要牢记7点，轻轻松松
 【线性代数及其应用 —— 第一章线性代数中的线性方程组】-1.线性方程组
 javascript 文本框中的数据丢失格式,导致没有换行,显示成一行,flask不显示本地图片问题
 【付费推广】常见问题合集，搜索推广FAQ 2
21 移动网络的前世今生
 Java：初级Java开发人员的顶级技能和主要职责
 Django使用post和get方法做简易登录验证
原文地址：https://blog.csdn.net/m0_46521579/article/details/133659504

一、伯努利随机过程

二、一维随机游动

1. 一维随机游动的位置概率