MATLAB中norm函数用法

目录

语法

说明

示例

向量模

向量的 1-范数

两个点之间的欧几里德距离

矩阵的 2-范数

N 维数组的 Frobenius 范数

常规向量范数

---

        norm函数的功能是计算向量范数和矩阵范数。

语法

n = norm(v)
n = norm(v,p)
n = norm(X)
n = norm(X,p)
n = norm(X,"fro")

说明

​n = norm(v) 返回向量 v 的欧几里德范数。此范数也称为 2-范数、向量模或欧几里德长度。

n = norm(v,p) 返回广义向量 p 范数。​

n = norm(X) 返回矩阵 X 的 2-范数或最大奇异值，该值近似于 max(svd(X))。

n = norm(X,p) 返回矩阵 X 的 p-范数，其中 p 为 1、2 或 Inf：​

• ​如果 p = 1，则 n 是矩阵的最大绝对列之和。

• 如果 p = 2，则 n 近似于 max(svd(X))。此值等效于 norm(X)。

• 如果 p = Inf，则 n 是矩阵的最大绝对行之和。

​n= norm(X,"fro") 返回矩阵或数组 X 的 Frobenius 范数。​

示例

向量模

        创建一个向量并计算模。

v = [1 -2 3];
n = norm(v)
n = 3.7417

向量的 1-范数

        计算向量的 1-范数，该范数为元素模的总和。

v = [-2 3 -1];
n = norm(v,1)
n = 6

两个点之间的欧几里德距离

        计算两个点之间的距离作为向量元素之差的范数。创建两个向量，表示欧几里德平面上两个点的 (x,y) 坐标。

a = [0 3];
b = [-2 1];

        使用 norm 来计算点之间的距离。

d = norm(b-a)
d = 2.8284

在几何学上，点之间的距离等于从一个点延伸到另一个点的向量的模。

矩阵的 2-范数

        计算矩阵的 2-范数，该范数为最大奇异值。

X = [2 0 1;-1 1 0;-3 3 0];
n = norm(X)
 
 
n = 4.7234

N 维数组的 Frobenius 范数

        计算一个 4 维数组X 的 Frobenius 范数，它等效于列向量 X(:) 的 2-范数。

X = rand(3,4,4,3);
n = norm(X,"fro")
n = 7.1247

        Frobenius 范数对于稀疏矩阵也很有用，因为 norm(X,2) 不支持稀疏 X。

欧几里德范数

        具有N个元素的向量v的欧几里德范数（也称为向量模、欧几里德长度或 2-范数）的定义如下：

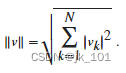
常规向量范数

        具有 N 个元素的向量 v 的 p-范数的常规定义是

其中 p 是任何正的实数值、Inf 或 -Inf。

• 如果 p = 1，则所得的 1-范数是向量元素的绝对值之和。

• 如果 p = 2，则所得的 2-范数是向量的模或欧几里德长度。

• 如果 p = Inf，则 ‖v‖∞=maxi(∣v(i)∣)。

• 如果 p = -Inf，则 ‖v‖−∞=mini(∣v(i)∣)。

最大绝对列之和

        m×n 矩阵 X (m,n >= 2) 的最大绝对列之和由

最大绝对行之和

        m×n 矩阵 X (m,n >= 2) 的最大绝对行之和由

Frobenius 范数

        m×n 矩阵 X (m,n >= 2) 的 Frobenius 范数由

定义

        此定义自然也适合扩展到二维以上的数组。例如，如果 X 是 N 维数组，大小为 m×n×p×...×q，则 Frobenius 范数为

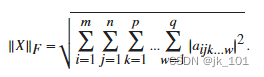
提示

• ​使用 vecnorm 将矩阵或数组视为向量的集合并计算指定维度上的范数。例如，vecnorm 可以计算矩阵中每列的范数。​