【算法】归并排序 详解

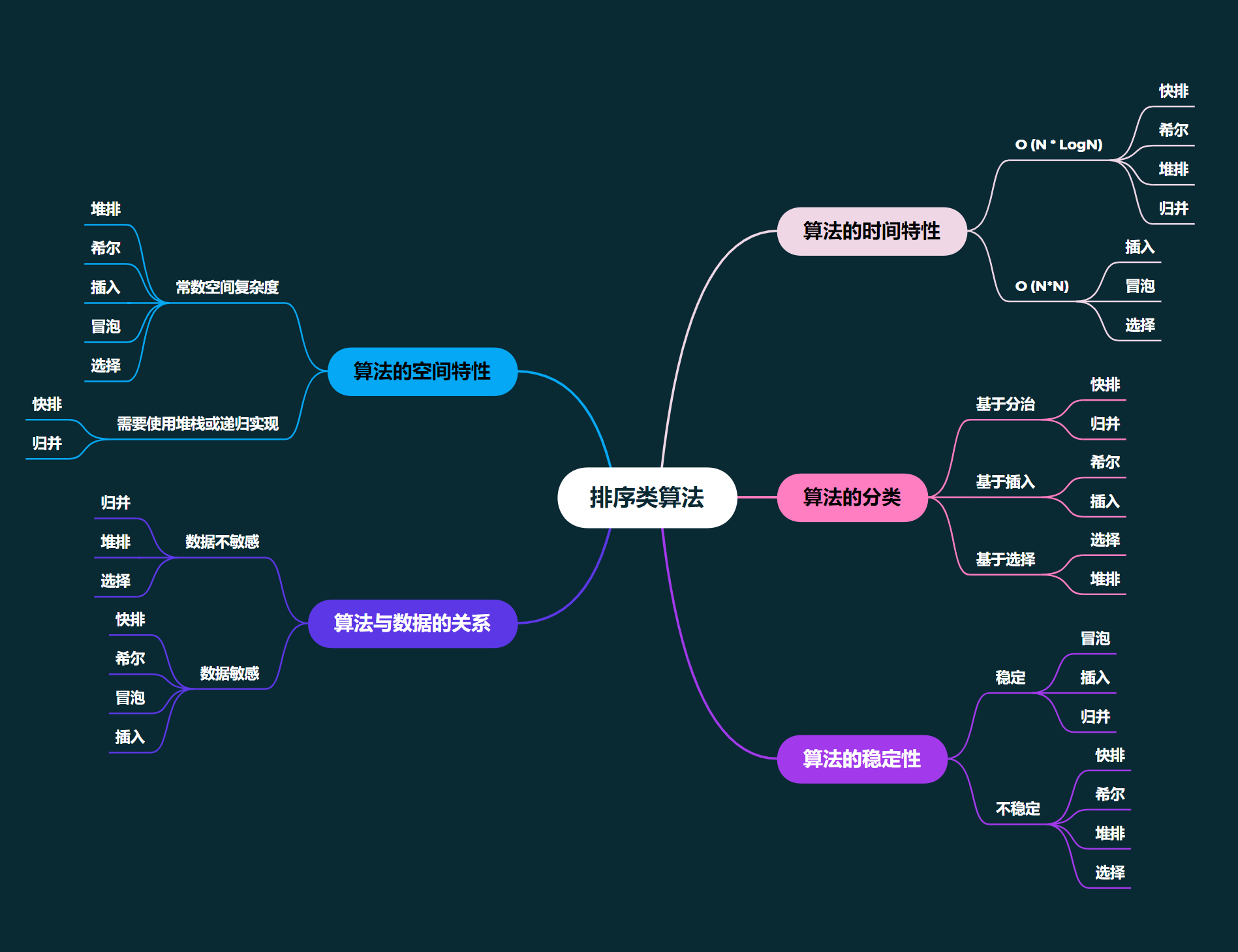
排序： 排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

稳定性： 假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中， r[i] = r[j]， 且 r[i] 在 r[j] 之前，而在排序后的序列中， r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的；否则称为不稳定的。
（注意稳定排序可以实现为不稳定的形式， 而不稳定的排序实现不了稳定的形式）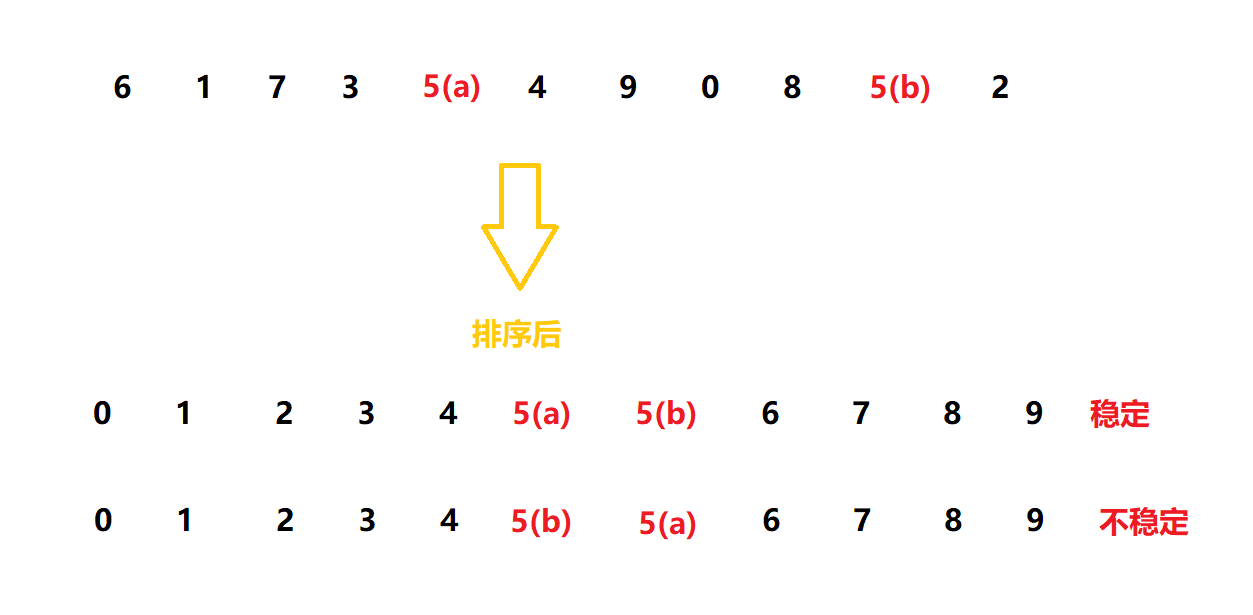

内部排序： 数据元素全部放在内存中的排序。

外部排序： 数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

归并排序

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤：

• 分解（Divide）：将n个元素分成两个个含n/2个元素的子序列。
• 解决（Conquer）：用合并排序法对两个子序列递归的排序。
• 合并（Combine）：合并两个已排序的子序列已得到排序结果。

代码实现

1. 递归版本

	public static void mergeSort(int[] arr) {
        int len = arr.length;
        partition(arr, 0, len-1);
    }


    public static void partition(int[] arr, int left, int right) {
        if (left >= right) {
            return;
        }
        // 将区间分成左右两个部分, 并将两个部分分别排序
        int mid = ((right-left) >> 1) + left;
        partition(arr, left, mid);
        partition(arr, mid+1, right);
        // 将两部分合并
        int[] temp = new int[right-left+1];
        int index = 0;
        int index1 = left;
        int index2 = mid+1;
        while (index1 <= mid && index2 <= right) {
            if (arr[index1] < arr[index2]) {
                temp[index++] = arr[index1++];
            } else {
                temp[index++] = arr[index2++];
            }
        }
        while (index1 <= mid) {
            temp[index++] = arr[index1++];
        }
        while (index2 <= right) {
            temp[index++] = arr[index2++];
        }
        // 重新拷贝回去
        for (int i = 0; i < index; i++) {
            arr[left+i] = temp[i];
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

2. 非递归版本

    public static void mergeSortNonR(int[] arr) {
        int len = arr.length;
        // i 表示的是, 左右区间中每个区间的元素个数
        for (int i = 1; i < len; i*=2) {
            // j 每次要跳过两个区间
            for (int j = 0; j < len; j += 2*i) {
                int left1 = j;
                int right1 = j + i - 1;
                int left2 = right1 + 1;
                int right2 = left2 + i - 1;
                // 修正一下 right1, right2, 因为可能 right1 和 right2 越界了
                if (right1 >= len) {
                    right1 = len-1;
                }
                if (right2 >= len) {
                    right2 = len - 1;
                }
                // 开始合并
                int[] temp = new int[2*i];
                int index = 0;
                while (left1 <= right1 && left2 <= right2) {
                    if (arr[left1] <= arr[left2]) {
                        temp[index++] = arr[left1++];
                    } else {
                        temp[index++] = arr[left2++];
                    }
                }
                while (left1 <= right1) {
                    temp[index++] = arr[left1++];
                }
                while (left2 <= right2) {
                    temp[index++] = arr[left2++];
                }
                // 拷贝回去
                for (int k = 0; k < index; k++) {
                    arr[j+k] = temp[k];
                }
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

总结：

• 时间复杂度： O（N*logN）
• 空间复杂度： O（N）
• 是稳定排序
• 对数据不敏感： 不管数据原本怎么排列, 都需要先分解, 然后归并。
• 归并的缺点在于需要 O(N) 的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。

海量数据的排序问题
假设条件为：内存只有 1G，需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下，所以需要外部排序，而归并排序是最常用的外部排序

1. 先把文件切分成 200 份，每个 512 M
2. 分别对 512 M 排序，因为内存已经可以放的下，所以任意排序方式都可以
3. 进行 2 路归并，同时对 200 份有序文件做归并过程，最终结果就有序了

以上就是对归并排序的讲解， 希望能帮到你 ！
评论区欢迎指正 ！