数据结构入门-13-图

一、图的概述

1.1 图论的作用

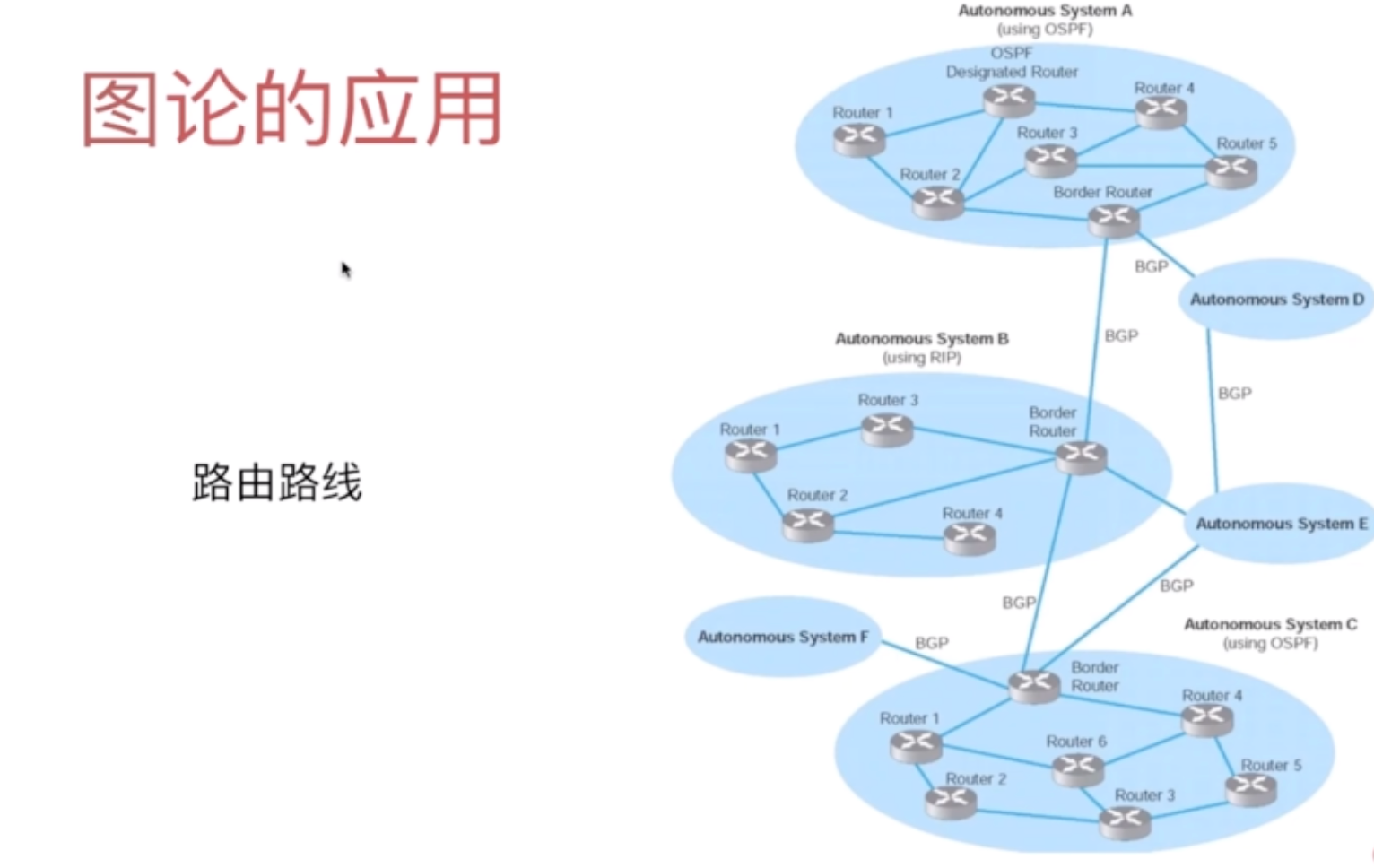
1.2 图的分类

1.2.1 无向图

1.2.2 有向图

1.2.3 无权图

1.2.4 有劝图

1.3 图的基本概念

1. 两点相邻
2. 点的邻边
3. 路径Path，从一个点到另一个点走过的路
4. 环Loop，多个点围城一个圈
5. 自环边，自己和自己形成环
6. 平行边，重复的边

7. 联通分量
   

8. 无环图
   
   树是一种无环图，一个联通的无环图(一个联通分量)就是树

9. 连通图的 生成树
   
   V：顶点数

10) 顶点的度degree
顶点相邻的边数

二、树的基本表示

2.1 邻接矩阵

V：顶点数，E：边数

2.1.1 邻接矩阵 表示图

import java.io.*;
import java.util.Scanner;

public class AdjMatrix {

    private int V;
    private int E;
    private int[][] adj;

    public AdjMatrix(String filename){

        File file = new File(filename);

        try(Scanner scanner = new Scanner(file)){

            V = scanner.nextInt();
            adj = new int[V][V];

            E = scanner.nextInt();
            for(int i = 0; i < E; i ++){
                int a = scanner.nextInt();
                int b = scanner.nextInt();
                adj[a][b] = 1;
                adj[b][a] = 1;
            }
        }
        catch(IOException e){
            e.printStackTrace();
        }
    }

    @Override
    public String toString(){
        StringBuilder sb = new StringBuilder();

        sb.append(String.format("V = %d, E = %d\n", V, E));
        for(int i = 0; i < V; i ++){
            for(int j = 0; j < V; j ++)
                sb.append(String.format("%d ", adj[i][j]));
            sb.append('\n');
        }
        return sb.toString();
    }

    public static void main(String[] args){

        AdjMatrix adjMatrix = new AdjMatrix("src/main/java/hGraph/base/file/g.txt");
        System.out.print(adjMatrix);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

    public int V(){
        return V;
    }

    public int E(){
        return E;
    }

//判断是否有边，两顶点是否相邻
    public boolean hasEdge(int v, int w){
        validateVertex(v);
        validateVertex(w);
        return adj[v][w] == 1;
    }
//查找和顶点v相连的顶点
    public ArrayList<Integer> adj(int v){
        validateVertex(v);
        ArrayList<Integer> res = new ArrayList<>();
        for(int i = 0; i < V; i ++)
            if(adj[v][i] == 1)
                res.add(i);
        return res;
    }
//查找顶点的度
    public int degree(int v){
        return adj(v).size();
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

2.1.2 邻接矩阵的复杂度

空间复杂度 可以优化，
求一个点的相邻结点 可以优化

稀疏图&稠密图
根据边的多少

完全图 每个顶点都连接

2.2 邻接表

2.2.1 邻接表的复杂度

2.2.2 邻接表By哈希表

用红黑树实现图

import java.io.File;
import java.io.IOException;
import java.util.TreeSet;
import java.util.Scanner;

public class AdjSet {

    private int V;
    private int E;
    private TreeSet<Integer>[] adj;

    public AdjSet(String pathStr){

        File file = new File(pathStr);

        try(Scanner scanner = new Scanner(file)){

            V = scanner.nextInt();
            if(V < 0) throw new IllegalArgumentException("V must be non-negative");
            adj = new TreeSet[V];
            for(int i = 0; i < V; i ++)
                adj[i] = new TreeSet<Integer>();

            E = scanner.nextInt();
            if(E < 0) throw new IllegalArgumentException("E must be non-negative");

            for(int i = 0; i < E; i ++){
                int a = scanner.nextInt();
                validateVertex(a);
                int b = scanner.nextInt();
                validateVertex(b);

                if(a == b) throw new IllegalArgumentException("Self Loop is Detected!");
                if(adj[a].contains(b)) throw new IllegalArgumentException("Parallel Edges are Detected!");

                adj[a].add(b);
                adj[b].add(a);
            }
        }
        catch(IOException e){
            e.printStackTrace();
        }
    }

    private void validateVertex(int v){
        if(v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + "is invalid");
    }

    public int V(){
        return V;
    }

    public int E(){
        return E;
    }

    public boolean hasEdge(int v, int w){
        validateVertex(v);
        validateVertex(w);
        return adj[v].contains(w);
    }

    public Iterable<Integer> adj(int v){
    // public TreeSet adj(int v){
        validateVertex(v);
        return adj[v];
    }

    public int degree(int v){
        validateVertex(v);
        return adj[v].size();
    }

    @Override
    public String toString(){
        StringBuilder sb = new StringBuilder();

        sb.append(String.format("V = %d, E = %d\n", V, E));
        for(int v = 0; v < V; v ++){
            sb.append(String.format("%d : ", v));
            for(int w : adj[v])
                sb.append(String.format("%d ", w));
            sb.append('\n');
        }
        return sb.toString();
    }

    public static void main(String[] args){

        AdjSet adjSet = new AdjSet("g.txt");
        System.out.print(adjSet);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95

三、图的深度优先遍历

3.1 图深度遍历过程

之前描述过树的遍历

    public GraphDFS(Graph G){

        this.G = G;
        visited = new boolean[G.V()];
        dfs(0);
    }

    private void dfs(int v){

        visited[v] = true;
        order.add(v);
        for(int w: G.adj(v))
            if(!visited[w])
                dfs(w);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

3.2 图遍历改进

不和0 相连 的顶点，就不会遍历
原因是只针对0 调用
改进：对每一个节点进行调用

    public GraphDFS(Graph G){

        this.G = G;
        visited = new boolean[G.V()];
        for(int v = 0; v < G.V(); v ++)
            if(!visited[v])
                dfs(v);
    }

    private void dfs(int v){

        visited[v] = true;
        pre.add(v);
        for(int w: G.adj(v))
            if(!visited[w])
                dfs(w);
        post.add(v);
    }

    public Iterable<Integer> pre(){
        return pre;
    }

    public Iterable<Integer> post(){
        return post;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

3.3 先中后

在树中有先中后遍历

图也可以分为 先 后序遍历

3.4 复杂度

遍历的复杂度：O(V+E)

四、深度遍历的应用

4.1 求联通分量

4.2 单源路径问题

依然做了深度优先遍历，记录这个顶点的pre：从哪里来的
单源路径：从一个顶点出发的路径，不能反向查找

import java.util.ArrayList;
import java.util.Collections;

public class SingleSourcePath {

    private Graph G;
    private int s;

    private boolean[] visited;
    private int[] pre;

    public SingleSourcePath(Graph G, int s){

        G.validateVertex(s);

        this.G = G;
        this.s = s;
        visited = new boolean[G.V()];
        pre = new int[G.V()];

        dfs(s, s);
    }

    private void dfs(int v, int parent){

        visited[v] = true;
        pre[v] = parent;
        for(int w: G.adj(v))
            if(!visited[w])
                dfs(w, v);
    }

    public boolean isConnectedTo(int t){
        G.validateVertex(t);
        return visited[t];
    }

    public Iterable<Integer> path(int t){

        ArrayList<Integer> res = new ArrayList<Integer>();
        if(!isConnectedTo(t)) return res;

        int cur = t;
        while(cur != s){
            res.add(cur);
            cur = pre[cur];
        }
        res.add(s);

        Collections.reverse(res);
        return res;
    }

    public static void main(String[] args){

        Graph g = new Graph("g.txt");
        SingleSourcePath sspath = new SingleSourcePath(g, 0);
        System.out.println("0 -> 6 : " + sspath.path(6));
        System.out.println("0 -> 5 : " + sspath.path(5));
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

4.3 检测无向图中的环

4.4 二分图检测

二分图：

五、图的广度优先遍历

    public GraphBFS(Graph G){

        this.G = G;
        visited = new boolean[G.V()];
        for(int v = 0; v < G.V(); v ++)
            if(!visited[v])
                bfs(v);
    }

    private void bfs(int s){

        Queue<Integer> queue = new LinkedList<>();
        queue.add(s);
        visited[s] = true;
        while(!queue.isEmpty()){
            int v = queue.remove();
            order.add(v);

            for(int w: G.adj(v))
                if(!visited[w]){
                    queue.add(w);
                    visited[w] = true;
                }
        }
    }

    public Iterable<Integer> order(){
        return order;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

复杂度：O(V+E)

六、图论问题的建模

七、图论和AI

十一、最小生成树

11.1 带权图

/// 暂时只支持无向带权图
public class WeightedGraph implements Cloneable{

    private int V;
    private int E;
    private TreeMap<Integer, Integer>[] adj;

    public WeightedGraph(String filename){

        File file = new File(filename);

        try(Scanner scanner = new Scanner(file)){

            V = scanner.nextInt();
            if(V < 0) throw new IllegalArgumentException("V must be non-negative");
            adj = new TreeMap[V];
            for(int i = 0; i < V; i ++)
                adj[i] = new TreeMap<Integer, Integer>();

            E = scanner.nextInt();
            if(E < 0) throw new IllegalArgumentException("E must be non-negative");

            for(int i = 0; i < E; i ++){
                int a = scanner.nextInt();
                validateVertex(a);
                int b = scanner.nextInt();
                validateVertex(b);
                int weight = scanner.nextInt();

                if(a == b) throw new IllegalArgumentException("Self Loop is Detected!");
                if(adj[a].containsKey(b)) throw new IllegalArgumentException("Parallel Edges are Detected!");

                adj[a].put(b, weight);
                adj[b].put(a, weight);
            }
        }
        catch(IOException e){
            e.printStackTrace();
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

十二、最短路径

带权图的最短路径不一定 走的边最少

12.1 迪杰斯特拉算法

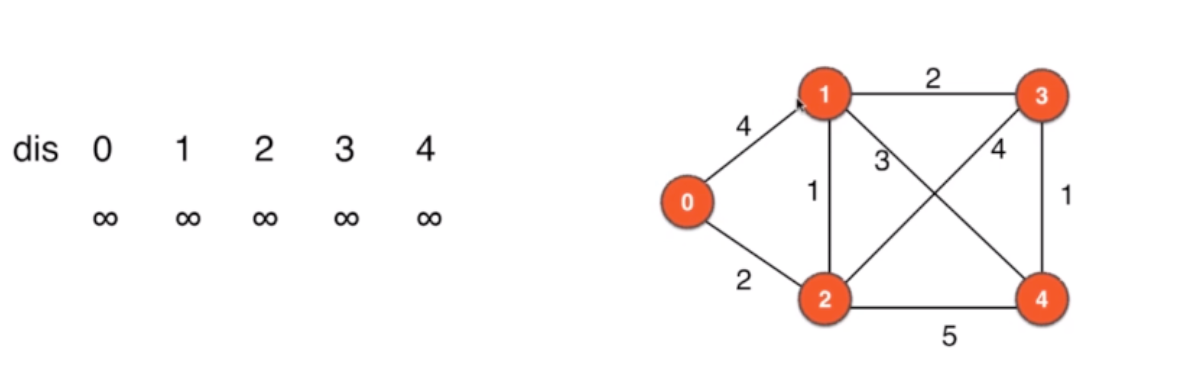
12.1.1 Dijkstra原理

1. 指定dis：源到各个顶点的路径，先初始为MAX
   

2. 找顶点，更新dis
   

3. 找当前最短的路径，确定这个就是到顶点的最短路径：确定2位0到2的最短路径
   

4. 根据2顶点，来做更新
   
   这里更新了2 到各个顶点的路径，1 从 4 更新到了3

5. 再从当前的路径中找最小的，为3 顶点1，
   所以确定顶点1 的最短路径为3

6. 再根据顶点1 ，更新dis
   
7. 确定当前最短的距离为5 ，顶点3
   
8. 更新dis，到顶点4都为6

每轮循环：

1. 初始化源到其他顶点的dis，默认都为MAX
2. 找到当前没有访问的最短路节点
3. 确定这个节点的最短路径就是当前大小
4. 根据这个节点的最短路径大小，更新到其他节点的路径长度，如果比dis中的要小，那么就更新dis

#from ChatGPT
1.初始化距离数组dist和标记数组visited。将起始地点设置为起点，其他地点的距离初始化为无穷大，visited数组初始化为false。
2.从起点开始遍历所有地点，选择当前距离最小且未被访问过的地点u。
3.对于地点u，更新与其相邻的地点v的距离，如果新的距离小于原来的距离，则更新距离数组dist和路径数组path。
4.标记地点u为已访问，重复上述过程，直到所有地点都被访问。
5.最终得到起点到每个地点的最短距离和路径。
1
2
3
4
5
6