并查集知识梳理

并查集

目录

• 并查集
  • 并查集的定义
  • 并查集的思想
  • 朴素并查集的代码
    • • （1）初始化
      • （2）查找
      • （3）合并
  • 路径压缩
    • • （1）查找代码
      • （2）路径压缩完整代码
  • 按秩合并
    • 思想
    • 实现
      • （1）初始化
      • （2）合并
  • 习题
• 完结撒花

这一章中用到里树的基础知识，不懂的朋友看这里

并查集的定义

1. 并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。
2. 并查集通常包含两种操作：
   查找(Find)：查询两个元素是否在同一个集合中
   合并(Union)：把两个不相交的集合合并为一个集合
3. 组词解释法：并：合并，查：查找，集：集合。连成一句话来说就是用来合并、查找的集合

并查集的思想

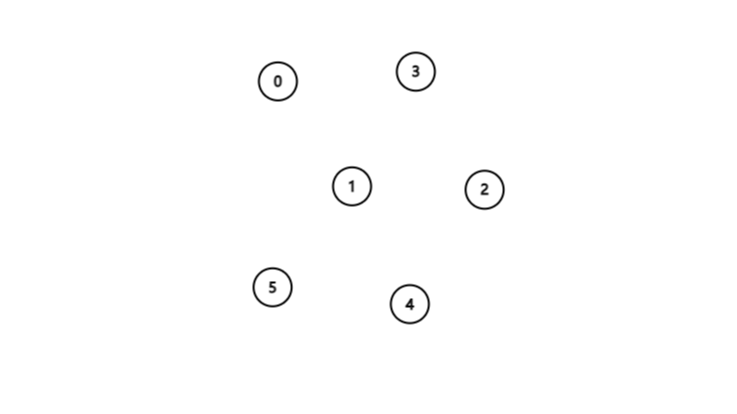
开始所有点上级都为它本身

下标	0	1	2	3	4	5
上级	0	1	2	3	4	5

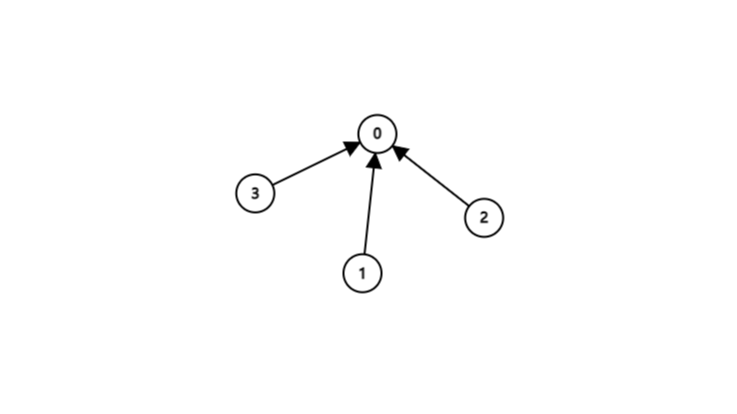
把2，3合并到0(树1)，

把4，5合并到1(树2)

下标	0	1	2	3	4	5
上级	0	1	0	0	1	1

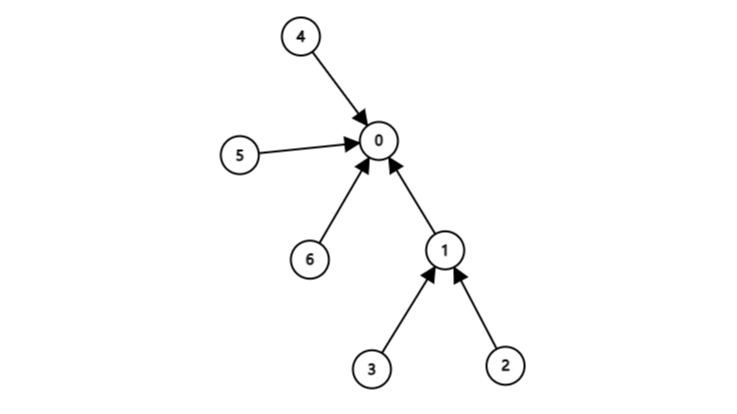
把1合并到0（合并树1，树2）

下标	0	1	2	3	4	5
上级	0	0	0	0	1	1

朴素并查集的代码

（1）初始化

highlighter- code-theme-dark Java

int parent[105];//记录自己的上级
void init(int n) {
    for(int i = 0;i < n;i ++) {
        parent[i] = i;//将自己的上级赋值为自己
    }
}

现在所有点上级都为它本身

下标	0	1	2	3	4	5
上级	0	1	2	3	4	5

（2）查找

highlighter- code-theme-dark Java

int find(int x) {
    if(parent[x] == x) {//判断自己是不是自己的上级
        return x;
    } else {
        return find(parent[x]);//如果不是，查找自己上级的上级
    }
}

查找时要一层一层的访问自己的上级，自己到自己是自己的上级为止

下标	0	1	2	3	4	5
上级	0	0	0	0	1	1

举例：访问4的上级

路径：4->1,1->0

（3）合并

highlighter- code-theme-dark Java

//把j合并到i中去
void merge(int i,int j) {
    parent[find(j)]=find(i);//把j的上级设为i的上级
}

下标	0	1	2	3	4	5
上级	0	1	0	0	1	1

下标	0	1	2	3	4	5
上级	0	0	0	0	1	1

将1合并到0
学到这里我们来看一看擒贼先擒王(记得先动手自己做）

路径压缩

作用:

​ 提高并查集效率

举一个极端的例子：

假设我们一共有1e9个点，如图一直排列下去

那么我们查找就需要o(n)的复杂度（就会爆炸）

但办法是人想出来的，记住并查集是一个树形结构，然后就有了下图的优化

这样一来时间复杂度就只有o(logn)了（十分的诱人呢）

接下来是上代码时间

（1）查找代码

版本一：

highlighter- code-theme-dark Java

int find (int x) {
    if (parent[x] == x) {
       return x; 
    } else {
        parent[x] = find(parent[x]);
        return parent[x];
    }
}

版本二：

highlighter- code-theme-dark Java

int find (int x) {
    return x == parent[x] ? x : (parent[x] = find(parent[x]));
}

（2）路径压缩完整代码

highlighter- code-theme-dark JavaScript

#include
using namespace std;
#define MAXN 100;
int parent[MAXN];
void init (int n) {//初始化
    for (int i = 1;i <= n;i ++){
        parent[i] = i;
    }
}
int find (int x) {//查找
    if (parent[x] == x) {
       return x; 
    } else {
        parent[x] = find(parent[x]);
        return parent[x];
    }
}
void merge (int i,int j) {//合并
    parent[j] = find(i);
}
int main() {
    return 0;
}

按秩合并

思想

如果现在要合并两一棵树，那么我们应该怎么去合并最优呢？

是从右边到左边？还是从左边到右边？谁是合并后的根节点？

显然这种情况下，我们有两种合并方法：

方法一：

方法二：

我们通过路径压缩知道，深度越浅时间复杂度的上限越小

所以，明显方法二才是最优解

实现

（1）初始化

highlighter- code-theme-dark Java

void init(int n) {
    for(int i = 0;i < n;i ++) {
        parent[i] = i;
        rank[i] = 1;//rank用来记录深度，开始一为一棵树，所以赋值为1
    }
}

（2）合并

highlighter- code-theme-dark Java

void merge (int i,int j) {//合并
    int x = find(i),y = find(j);
    if(rank[x] < rank[y]) {//x作为根节点和y作为根节点的子树的深度比较
        parent[x] = y;//小于则把x合并到y
    } else {
        parent[y] = x;//大于则把y合并到x
    }
    if(rank[x] == rank[y] && x != y) {
        rank[x] ++;//如果两棵树深度相同，那么rank[x] + 1;
    }
}

习题

「NOI2015」程序自动分析
「JSOI2008」星球大战
「NOI2001」食物链
「NOI2002」银河英雄传说

完结撒花

欢迎大家留言
小编蒟蒻一个，有什么问题请大佬不惜赐教Orz

• 并查集
•     并查集的定义
•     并查集的思想
•     朴素并查集的代码
•             （1）初始化
•             （2）查找
•             （3）合并
•     路径压缩
•             （1）查找代码
•             （2）路径压缩完整代码
•     按秩合并
•         思想
•         实现
•             （1）初始化
•             （2）合并
•     习题
• 完结撒花

__EOF__