使用pytorch进行FFT和STFT

首先，我们定义一个波形，幅值分别为20和38，频率为2和13：
$$y=20\sin (2\pi \times 2x)+38\sin (2\pi \times 13x)$$
采样频率为200Hz，采样时间为1s。由于Pytorch中没有类似于Numpy中numpy.pi的用法，所以我们先用Numpy计算函数，然后再存入Tensor。

import torch
import numpy as np
import matplotlib.pyplot as plt

Fs = 200 # Sampling frequency
T = 1 / Fs # period
t = 1 # time
L = Fs * t # signle length

x = np.arange(L)*T
y = 20*np.sin(2*np.pi*2*x) + 38*np.sin(2*np.pi*13*x)

plt.plot(x,y)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

波形图如下：

傅里叶变换是一种将信号从时域转换到频域的数学工具。它将一个连续或离散的信号分解成一系列不同频率的正弦和余弦波的叠加。使用pytorch对该函数进行快速傅里叶变换：

p = torch.fft.fft(torch.from_numpy(y))
p = 2 * torch.abs(p) / len(p)
p = p[:int(len(p) / 2)]
p[0] = 0.
freq_bin = np.arange(int(L/2))*Fs/L

plt.plot(freq_bin,p)
plt.xlabel('Frequency (Hz)')
plt.ylabel('|P1|')
plt.show()
1
2
3
4
5
6
7
8
9
10

频谱图如下，可以看到幅值和频率与函数y相同：

下面，我们再对函数进行短时傅里叶变换。短时傅里叶变换（Short-Time Fourier Transform，STFT）是一种信号处理技术，用于将非平稳信号分解成时间和频率的分量。它是傅里叶变换（Fourier Transform）的一种变体，在时间上加一定的窗函数，然后对每个窗函数内的信号进行傅里叶变换，从而得到时频域上的信号特征。STFT常用于音频、图像等信号处理领域，以提取时域和频域上的信息，以及信号的时频分布特性：

spectrum = torch.stft(input=torch.from_numpy(y), n_fft=200, return_complex=True)
1

此外，还可以用torchaudio.functional.spectrogram，也是返回STFT之后的频谱。

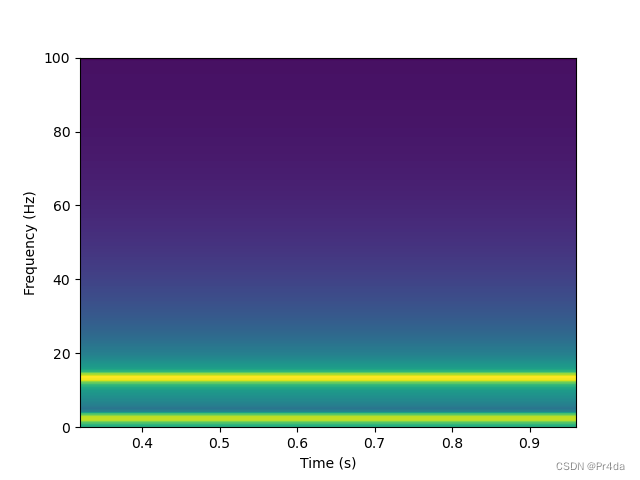
如果想直接画出频谱图可以使用matplotlib的plt.specgram方法：

plt.specgram(y, Fs=Fs)
plt.xlabel('Time (s)')
plt.ylabel('Frequency (Hz)')
plt.show()
1
2
3
4

效果如下：