• 初阶数据结构学习记录——열셋 排序（2）

    目录

    一、霍尔法

    二、挖坑法

    三、双指针法

    四、非递归快排

    一、霍尔法

    接着上一篇说快排

    改进一下上一篇所写的快排。

    1. void QuickSort(int* a, int begin, int end)//用begin和end来表示区间
    2. {
    3.     if (begin >= end)
    4.     {
    5.         return;
    6.     }
    7.     int left = begin, right = end;
    8.     int key = left;//最终要换的时候跟最左边的换，所以这里=left
    9.     while (left < right)
    10.     {
    11.         while (left < right && a[right] >= a[key])
    12.         {
    13.             right--;
    14.         }
    15.         while (left < right && a[left] <= a[key])
    16.         {
    17.             left++;
    18.         }
    19.         Swap(&a[left], &a[right]);
    20.     }
    21.     Swap(&a[left], &a[key]);
    22.     key = left;
    23.     //[begin, key - 1]  [key + 1, end]
    24.     QuickSort(a, begin, key - 1);
    25.     QuickSort(a, key + 1, end);
    26. }

    这里的快排方法是霍尔方法。不过这个方法还没完全。可以发现，排一遍后，就会分成两个区间继续快排，然后左右两个区间又会各自分出两个区间继续排，所以这其实是一个满二叉树结构，每个区间不一定都需要排。

    现在这个算法的时间复杂度是多少？如果单趟排序，那么应该是一个O(N)。具体应该走多少次？

    这个二叉树结构的高度是logN，数据总数为N。第一次排序后，到了第二层，左右两个区间继续排，这时候要排的数据总数就变成N - 1。第三层就变成了N -  3，然后一直排下去。不过持续减下去N也不会减到0，假设N是1000，那么总体的高度大约就是10，所以最终N也没减少太多。

    所以整体时间复杂度应该是N * logN。不过快排的时间复杂度也并非是这个，毕竟不可能每次都在排序。对于快排来说，无论是顺序还是逆序，似乎每一次都要排序，这时候的时间复杂度可以看出来是N^2，所以有序对于快排来讲就是很不好的情况，相反，无序才是快排最适合的。不过实际中我们无法决定数据是什么序。假如是逆序或者顺序，选择前后两端作为key，都需要所有数据全部走一遍才行。为了解决这个问题，需要把key随机一下，在快排之前，先把最大最小以及中间那个数字拿出来做比较，选中杯，这样即使是一个有序的数据集，也不会每次都要全部比较排序一遍；这个方法放到无序数据里也没关系，这对无序并没有多少影响，当然也有可能在无序数据里就正好选出了最小的那个数，但概率确实小，不必考虑。

    我们看一下有序和无序数据快排的效率，先改成有序10万个数字。

    再改成无序

    这当然是在release模式下运行的，如果是在debug下运行，有序数据其实就崩了，因为现在这个快排是个递归写法，对于有序数组，代码需要一直往下开栈，开到最后才停，所以栈爆了。而且，仅从数字上看也能看出，快排面对有序或者接近有序是低效的。

    现在我们写一下三数取中算法。不过确定中间值后key还是=begin，只是在这之前把中间值和begin的值互换一下。

    1. int GetMidIndex(int* a, int begin, int end)
    2. {
    3.     int mid = (begin + end) / 2;
    4.     if (a[begin] < a[mid])
    5.     {
    6.         if (a[mid] < a[end])
    7.             return mid;
    8.         else if (a[begin] > a[end])
    9.             return begin;
    10.         else return end;
    11.     }
    12.     else
    13.     {
    14.         if (a[mid] > a[end])
    15.             return mid;
    16.         else if (a[begin] < a[end])
    17.             return begin;
    18.         else return end;
    19.     }
    20. }

    加入三数取中后，再看有序快排

     这就正常了。再看无序

     当然选key问题还有别的解决办法，比如选出随机数做key。

    选key结束后，现在这个快排还有另一个问题。快排会逐渐减少排序的数据量，如果N是10，排序两个层后每个区间也就剩两三个数据了，回想一下刚才说的二叉树结构，如果继续使用快排，那么又得选key， 继续调用栈帧，这样的话不高效啊，费空间，而且实际上10个数是一个很小的数据了，10个数我们还需要做好几次递归，小题大做了。所以小数据时就不用快排了，当然其他用递归的排序也不选了，冒泡和选择排序也先去掉，所以就剩直接插入，希尔，堆排序了。

    实际上会选择直接插入排序。希尔排序会先预排，让大的数尽快走到后面，然后再插入排序，不过小数据上希尔排序也不一定有优势。

    我们看一下10000个数排序

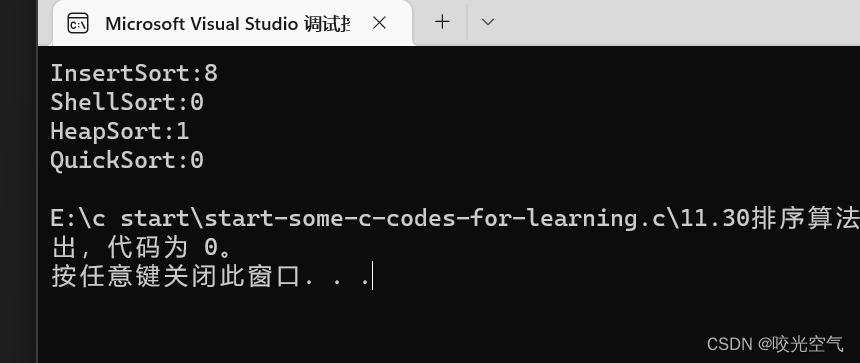
     所以总共就差距几毫秒而已。没必要再去做预排序了。而堆排序其实还要向下调整，建堆，所以不如简单的一个思路，直接插入即可。

    10个数的递归，是经历三层排序才会结束。如果这样的小数据用插入排序，实际上会省出很多的时间。按照二叉树结构，第一层递归1次，第二层2次，第三层4次，第4层8次，而最后一层就是2^h - 1。即使去掉最后一层，也会减少一半的递归次数，而去掉最后三层就去掉了80%多的次数。可以带入具体的数来计算，会发现最后一层占了一半，而倒数第二层大约占总次数的25%。所以小区间的优化很有必要。

    现在写一下代码

    1. void QuickSort(int* a, int begin, int end)
    2. {
    3.     if (begin >= end)
    4.     {
    5.         return;
    6.     }
    7.     if (end - begin + 1 < 15)
    8.     {
    9.         InsertSort(a + begin, end - begin + 1);
    10.     }
    11.     int mid = GetMidIndex(a, begin, end);
    12.     Swap(&a[begin], &a[mid]);
    13.     int left = begin, right = end;
    14.     int key = left;
    15.     while (left < right)
    16.     {
    17.         //右边先走，找小
    18.         while (left < right && a[right] >= a[key])
    19.         {
    20.             right--;
    21.         }
    22.         //左边再走，找大
    23.         while (left < right && a[left] <= a[key])
    24.         {
    25.             left++;
    26.         }
    27.         Swap(&a[left], &a[right]);
    28.     }
    29.     Swap(&a[left], &a[key]);
    30.     key = left;
    31.     QuickSort(a, begin, key - 1);
    32.     QuickSort(a, key + 1, end);
    33. }

     做一下测试，这里效果不如三数取中那么明显，所以我们取很大的数，就不看插入排序了。

    百万个数据 

    千万个

    千万个有序

     不过这里用的测试很单一，代码很简单，只是看一个大概的效果改变。以及release模式对于递归的优化也很大。

    debug下百万无序

     有序的话会更快

    不过千万个数据debug下就难受了。

    二、挖坑法

    快排其实不止这一个方法，这个方法是霍尔方法，而快排还有另外两个办法，挖坑和双指针。

    先把代码区分出来，三个方法都取名叫Partsort

    1. int PartSort1(int* a, int begin, int end)
    2. {
    3.     int mid = GetMidIndex(a, begin, end);
    4.     Swap(&a[begin], &a[mid]);
    5.     int left = begin, right = end;
    6.     int key = left;
    7.     while (left < right)
    8.     {
    9.         //右边先走，找小
    10.         while (left < right && a[right] >= a[key])
    11.         {
    12.             right--;
    13.         }
    14.         //左边再走，找大
    15.         while (left < right && a[left] <= a[key])
    16.         {
    17.             left++;
    18.         }
    19.         Swap(&a[left], &a[right]);
    20.     }
    21.     Swap(&a[left], &a[key]);
    22.     key = left;
    23.     return key;
    24. }
    25.  
    26. void QuickSort(int* a, int begin, int end)
    27. {
    28.     if (begin >= end)
    29.         return;
    30.     if ((end - begin + 1) < 15)
    31.     {
    32.         // 小区间用直接插入替代，减少递归调用次数
    33.         InsertSort(a + begin, end - begin + 1);
    34.     }
    35.     else
    36.     {
    37.         int keyi = PartSort1(a, begin, end);
    38.         QuickSort(a, begin, keyi - 1);
    39.         QuickSort(a, keyi + 1, end);
    40.     }
    41. }

    挖坑法依然要用到key，不过key的用法不一样，key会先存一个值，这个值对应的位置就形成一个坑位，然后左右LR开始走，R找到比key小的后，赋值给坑位，这样小的值就去了前面，R停的位置的值仍然没变，R形成新的坑位，然后L找比key大的值，赋值给坑位，那么大的值就去了后面，L处形成新的坑位。这个方法走完一次后的数据顺序和霍尔方法后的顺序不一样。

    这里还是要找中杯。这个方法和霍尔有些像，实现起来也不算难。

    1. // 挖坑法
    2. int PartSort2(int* a, int begin, int end)
    3. {
    4.     int mid = GetMidIndex(a, begin, end);
    5.     Swap(&a[begin], &a[mid]);
    6.  
    7.     int left = begin, right = end;
    8.     int key = a[left];
    9.     int hole = left;
    10.     while (left < right)
    11.     {
    12.         // 右边找小，填到左边坑里面
    13.         while (left < right && a[right] >= key)
    14.         {
    15.             --right;
    16.         }
    17.  
    18.         a[hole] = a[right];
    19.         hole = right;
    20.  
    21.         // 左边找大，填到右边坑里面
    22.         while (left < right && a[left] <= key)
    23.         {
    24.             ++left;
    25.         }
    26.  
    27.         a[hole] = a[left];
    28.         hole = left;
    29.     }
    30.  
    31.     a[hole] = key;
    32.     return hole;
    33. }

    三、双指针法

    双指针prev，cur，这个方法理解后代码就会很容易写出来。假设选择0下标为key，prev指向0，而cur指向1下标处。cur往后走，如果小于key，那么prev往后走一步，和cur互换一下；遇到大于key的值后，prev停下，cur继续往后走，等再次找到小的，那么prev往后走一步，来到一个大的值，互换一下。当然这里持续地往后走，我们一定要考虑越界问题，以及如果cur和prev处于同一位置，那么此时的互换可以避开一下，节省不必要的操作。

    当cur走到边界时，这次循环结束，而此时prev在最近一次互换好的位置上，比如712888812，假定key为7，那么prev就在第2个8的位置，当然此时应当是2，并且这时候的值一定小于key，这个位置的值和key互换，key得到这个下标，然后分成两个区间继续排序。

    1. //双指针
    2. int PartSort3(int* a, int begin, int end)
    3. {
    4.     int mid = GetMidIndex(a, begin, end);
    5.     Swap(&a[begin], &a[mid]);
    6.     int key = begin;
    7.     int prev = begin, cur = begin + 1;
    8.     while (cur <= end)
    9.     {
    10.         if (a[cur] < a[key] && ++prev != cur)
    11.             Swap(&a[prev], &a[cur]);
    12.         ++cur;
    13.     }
    14.     Swap(&a[prev], &a[key]);
    15.     key = prev;
    16.     return key;
    17. }

     两个swap之前和之后的代码暂且不管，重点在中间。cur一开始就在prev的后一步；++prev ！= cur就是避免同位置互换的操作。

    四、非递归快排

    以上都是递归排法，但毕竟需要一直开栈，所以非递归写法是很必要的。

    这个可以和斐波那契数列的做法相似，数列是把第一个第二个直接写了出来，然后循环，快排的非递归也是改循环，不过需要借助栈。

    先想一下递归。先递归左，然后回去再递归右，区间的变化是可以捕捉到的，用栈也一样，栈保存区间，我们就可以和递归一样访问不同的区间了。

    假设一个10个数的数组，栈里进去0和9下标后，先放进6和9，再放0和4，这样就能先改变[0, 4]区间的顺序了。

    1. void QuickSortNonR(int* a, int begin, int end)
    2. {
    3.     ST st;
    4.     StackInit(&st);
    5.     StackPush(&st, begin);
    6.     StackPush(&st, end);
    7.     while (!StackEmpty(&st))
    8.     {
    9.         int right = StackTop(&st);
    10.         StackPop(&st);
    11.         int left = StackTop(&st);
    12.         StackPop(&st);
    13.         int keyi = PartSort3(a, left, right);
    14.         // [left, keyi-1] keyi [keyi+1, right]
    15.         if (keyi + 1 < right)
    16.         {
    17.             StackPush(&st, keyi + 1);
    18.             StackPush(&st, right);
    19.         }
    20.  
    21.         if (left < keyi - 1)
    22.         {
    23.             StackPush(&st, left);
    24.             StackPush(&st, keyi - 1);
    25.         }
    26.     }
    27.     StackDestroy(&st);
    28. }

    栈中保留的始终是区间的两端。right拿到栈顶，也就是end，left拿到剩下的一个元素，也就是begin，选好key，就开始分区间排序。如果说走到最后，区间已经不存在了或者只存在一个值，那就不需要再push了，所以有两个if作为判断。只要栈中还有数据，我们就需要继续循环，所以while判断条件是不为空。整个过程也就结束了。

    到现在为止，所有排序的测试：

    1. void TestInsertSort()
    2. {
    3.     int a[] = { 9, 1, 2, 5, 7, 4, 8, 6, 3, 5 };
    4.     InsertSort(a, sizeof(a) / sizeof(int));
    5.     PrintArray(a, sizeof(a) / sizeof(int));
    6. }
    7.  
    8. void TestShellSort()
    9. {
    10.     int a[] = { 9, 1, 2, 5, 7, 4, 8, 6, 3, 5 };
    11.     //int a[] = { 9,8,7,6,5,4,3,2,1,0,5,4,2,3,6,2,0,2,1,-1,-2,-1,-3 };
    12.     PrintArray(a, sizeof(a) / sizeof(int));
    13.     ShellSort(a, sizeof(a) / sizeof(int));
    14.     PrintArray(a, sizeof(a) / sizeof(int));
    15. }
    16.  
    17. void TestSelectSort()
    18. {
    19.     int a[] = { 9, 1, 2, 5, 7, 4, 8, 6, 3, 5 };
    20.     SelectSort(a, sizeof(a) / sizeof(int));
    21.     PrintArray(a, sizeof(a) / sizeof(int));
    22. }
    23.  
    24. void TestBubbleSort()
    25. {
    26.     int a[] = { 9, 1, 2, 5, 7, 4, 8, 6, 3, 5 };
    27.     BubbleSort(a, sizeof(a) / sizeof(int));
    28.     PrintArray(a, sizeof(a) / sizeof(int));
    29. }
    30.  
    31. void TestQuickSort()
    32. {
    33.     int a[] = { 6,1,2,7,9,3,4,5,8,10,8 };
    34.     //int a[] = { 6, 1, 2, 7, 9, 3, 4, 5, 6, 8 };
    35.     QuickSort(a, 0, sizeof(a) / sizeof(int)-1);
    36.     //QuickSortNonR(a, 0, sizeof(a) / sizeof(int) - 1);
    37.     PrintArray(a, sizeof(a) / sizeof(int));
    38. }
    39.  
    40. void Test()
    41. {
    42.     srand(time(0));
    43.     const int N = 100000;
    44.     int* a1 = (int*)malloc(sizeof(int) * N);
    45.     int* a2 = (int*)malloc(sizeof(int) * N);
    46.     int* a3 = (int*)malloc(sizeof(int) * N);
    47.     int* a4 = (int*)malloc(sizeof(int) * N);
    48.     int* a5 = (int*)malloc(sizeof(int) * N);
    49.     int* a6 = (int*)malloc(sizeof(int) * N);
    50.  
    51.     int y = 0, z = 0;
    52.     for (int x = 0; x < N; ++x)
    53.     {
    54.         y = rand();
    55.         if (y % 4 == 0 || y % 7 == 0 || y % 47 == 0)
    56.         {
    57.             y += z;
    58.             ++z;
    59.         }
    60.         a1[x] = y;
    61.         a2[x] = a1[x];
    62.         a3[x] = a1[x];
    63.         a4[x] = a1[x];
    64.         a5[x] = a1[x];
    65.         a6[x] = a1[x];
    66.     }
    67.  
    68.     int begin1 = clock();
    69.     InsertSort(a1, N);
    70.     int end1 = clock();
    71.  
    72.     int begin2 = clock();
    73.     ShellSort(a2, N);
    74.     int end2 = clock();
    75.  
    76.     int begin3 = clock();
    77.     HeapSort(a3, N);
    78.     int end3 = clock();
    79.  
    80.     int begin4 = clock();
    81.     SelectSort(a4, N);
    82.     int end4 = clock();
    83.  
    84.     int begin5 = clock();
    85.     BubbleSort(a5, N);
    86.     int end5 = clock();
    87.  
    88.     int begin6 = clock();
    89.     QuickSort(a6, 0, N - 1);
    90.     //QuickSortNonR(a6, 0, N - 1);
    91.     int end6 = clock();
    92.  
    93.     printf("InsertSort:%d\n", end1 - begin1);
    94.     printf("ShellSort:%d\n", end2 - begin2);
    95.     printf("HeapSort:%d\n", end3 - begin3);
    96.     printf("SelectSort:%d\n", end4 - begin4);
    97.     printf("BubbleSort:%d\n", end5 - begin5);
    98.     printf("QuickSort:%d\n", end6 - begin6);
    99.  
    100.     free(a1);
    101.     free(a2);
    102.     free(a3);
    103.     free(a4);
    104.     free(a5);
    105.     free(a6);
    106. }
    107.  
    108. int main()
    109. {
    110.     //TestInsertSort();
    111.     //TestShellSort();
    112.     //TestSelectSort();
    113.     //TestBubbleSort();
    114.     //TestQuickSort();
    115.     Test();
    116.     return 0;
    117. }

    下一篇写归并排序。

    结束。

  • 相关阅读:
    WebVR
    IntelliJ IDE 插件开发指南
    swiper轮播嵌入视频
    面向对象-Python
    openstack 环境配置及基础组件安装
    21.State状态（行为型模式）
    CMake中configure_file的使用
    浅谈Elasticsearch 文档操作
    随笔一
    ubuntu 23.04从源码编译安装rocm运行tensorflow-rocm
  • 原文地址：https://blog.csdn.net/kongqizyd146/article/details/128162643