• WeetCode2滑动窗口系列

    一丶[无重复字符的最长子串](3. 无重复字符的最长子串 - 力扣（Leetcode）)#

    思路:#

    维护一个窗口，窗口中不存在重复的字符，窗口右边界从第一个字符移动到最后，使用一个变量记录窗口大小的最大值

    那么问题就变成了：怎么确保窗口中不存在重复的字符，我们可以使用一个set，每次发现right位置的字符A重复后，就一直移动到之前A字符位置的下一个。比如 BACDHA，此时right位于第二个A，set中包含字符BACDH，为了维持不重复，我们要将左边界移动到第一个C的位置，while循环让left右移，并删除left位置的字符，直到第一个A被删除

    继续思考下，其实没必要使用一个set，直接使用一个map即可，map需要记录字符和这个字符最近出现的位置,当前字符重复A的时候，就让left移动到A最近出现位置的前一个。比如BACDHA，此时right为A，map中记录了B->0，A->1等信息，我们只需要让left移动到1+1（A最近出现于下标1，left需要移动到2位置）然后再map中重新记录A->5即可

    代码：#

    1.    public int lengthOfLongestSubstring(String s) {
    2.        //空字符串
    3.         if(s==null||s.length()==0){
    4.             return 0 ;
    5.         }
    6.        
    7.        //窗口大小 最大值
    8.         int res = 0;
    9.        
    10.         int left = 0;
    11.         int right = 0;
    12.         int len = s.length();
    13.        
    14.        //key字符，value 这个字符最近在什么位置出现
    15.        HashMap<Character,Integer> recentLocation = new HashMap<>();
    16.  
    17.         while(right<len){
    18.             //当前子u发
    19.             char curChar = s.charAt(right);
    20. 			//获取这个字符出现的位置
    21.             Integer index = recentLocation.get(curChar);
    22. 			//如果不为null 说明这个字符曾经出现过 那么这时候需要 让left 移动
    23.             if(index!=null){
    24.                 left = Math.max(index+1,left);
    25.             }
    26.             //记录下最近的位置
    27.             recentLocation.put(curChar,right);
    28.             
    29.             right++;
    30.             
    31.             //窗口最大长度更新
    32.             res = Math.max(res,right-left);
    33.         }
    34.         return res;
    35.     }

    二丶[最小覆盖子串](76. 最小覆盖子串 - 力扣（Leetcode）)#

    思路：#

    使用一个Map表示当前滑动串口亏欠t中字符的数量， key 字符 value 当前窗口中亏欠的数目，亏欠的意思是当前窗口至少还需要多少个key的字符才满足t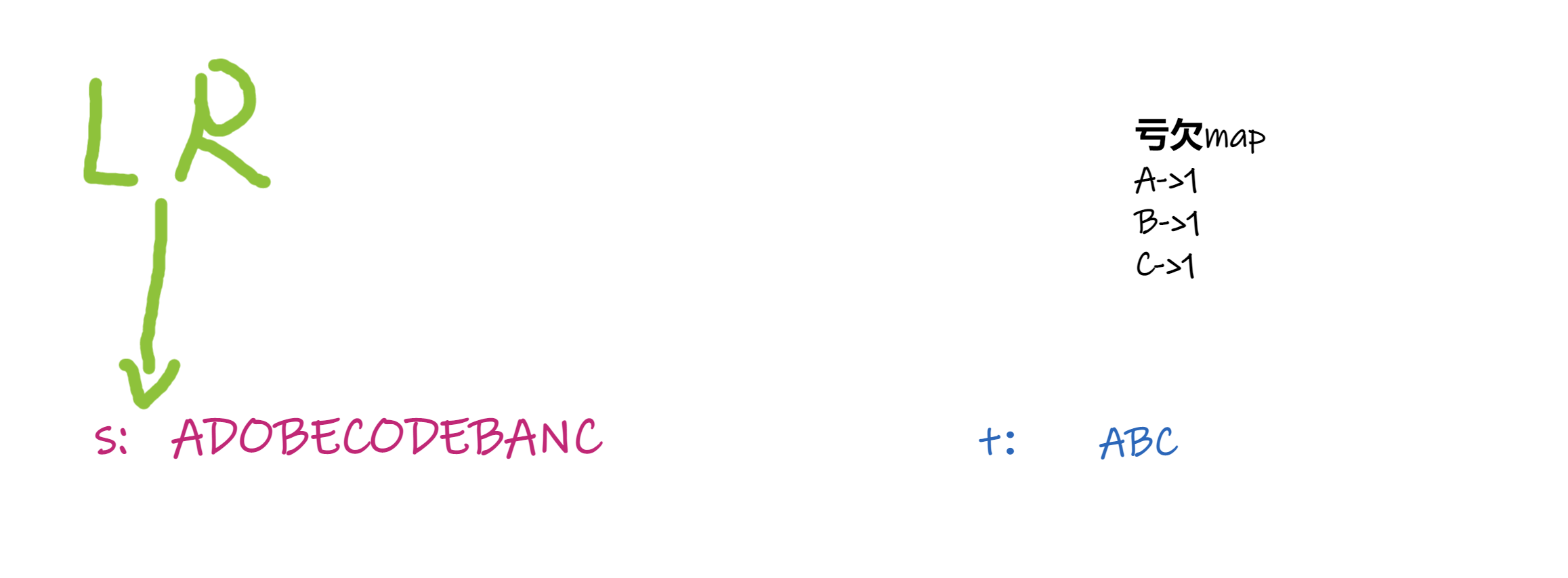

    当left小于right的时候，我们尽可能让left向右滑动，那么什么时候left可以向右滑昵？——当前left是一个t中根本不存在的字符，或者窗口中left位置的字符数量大于t中的数量（对应下面两图）（这其实是有贪心的思想在其中的，题目是找最短的，那么left越接近right 那么越短）并且亏欠map需要同时维护

    然后我们需要移动right指针，同时维护亏欠map

    那么什么时候窗口中满足要求包含了t中所有字符昵——亏欠map中不存在value大于0的entry，这时候我们需要更新最佳结果

    并且找到一个答案之后，我们需要left向右移动一个位置，并维护亏欠map，比如s=ADOBECODEBANC，t=ABC我们第一次找到符合的结果是ADOBEC，这时候需要left向右，因为后面存在更优秀的答案。

    代码：#

    1. class Solution {
    2.    public String minWindow(String s, String t) {
    3.  
    4.         //逆天用例
    5.         if (s == null || s.length() == 0) {
    6.             return null;
    7.         }
    8.     
    9.         if(s.length() < t.length()){
    10.             return "";
    11.         }
    12.  
    13.         
    14.     
    15.         char[] tCharArray = t.toCharArray();
    16.         // key 字符 value 当前窗口中亏欠的数目，亏欠的意思是当前窗口至少还需要多少个key的字符才满足t
    17.         // value 为正数 表示窗口欠 t，0表示互不亏欠，负数表示窗口中此字符数目多于t
    18.         Map<Character, Integer> owesCharCountMap = new HashMap<Character, Integer>();
    19.  
    20.         //初始化亏欠的数目
    21.         for (char loop : tCharArray) {
    22.             owesCharCountMap.put(loop, owesCharCountMap.getOrDefault(loop, 0) + 1);
    23.         }
    24.  
    25.  
    26.  
    27.         String res = null;
    28.         int left = 0;
    29.         int right = 0;
    30.  
    31.         while (right < s.length()) {
    32.  
    33.             //如果left对应字符是无关紧要的字符（t中不包含的字符）
    34.             //或者left对应的字符那怕删掉 窗口中的字符也不会亏钱t中的字符 
    35.             //满足上面任意一点 那么 left++
    36.             while (left < right && !isNecessary(left, s, owesCharCountMap)) {
    37.                 //当前left的字符
    38.                 char leftChar = s.charAt(left);
    39.                 left++;
    40.                 //当前窗口亏欠窗口中多少个
    41.                 Integer count = owesCharCountMap.get(leftChar);
    42.                 //如果不为null 说明leftChar 是t中的字符 
    43.                 if (count != null) {
    44.                     //亏欠数++
    45.                     owesCharCountMap.put(leftChar, count + 1);
    46.                 }
    47.             }
    48.  
    49.             //right位置的字符
    50.             char rightChar = s.charAt(right);
    51.  
    52.             //right位置字符 窗口亏欠的数目
    53.             Integer count = owesCharCountMap.get(rightChar);
    54.             //right处字符是一个t中的字符 那么亏欠数-1
    55.             if (count != null) {
    56.                 owesCharCountMap.put(rightChar, count - 1);
    57.             }
    58.  
    59.             //如果窗口满足要求——指最起码不欠t中字符，及包含了所有t中的字符，那怕存在富足
    60.             if (meetRequirementsOrNot(owesCharCountMap)) {
    61.  
    62.                 //sub以下
    63.                 String tempRes = s.substring(left, right + 1);
    64.                 //记录
    65.                 if (res == null || tempRes.length() < res.length()) {
    66.                     res = tempRes;
    67.                 }
    68.  
    69.                 //从窗口中 强制删除left位置处的字符
    70.                 //比如s=ADOBECODEBANC t = ABC 此时窗口中字符为ADOBEC 我们找到了一种结果，但是后续可能存在更好的答案
    71.                 //删除left位置的A 我们继续找更好的结果
    72.                 char leftChar = s.charAt(left);
    73.                 Integer leftCount = owesCharCountMap.get(leftChar);
    74.                 if (leftCount!=null){
    75.                     owesCharCountMap.put(leftChar,leftCount+1);
    76.                 }
    77.                 left++;
    78.             }
    79.             right++;
    80.  
    81.  
    82.         }
    83.  
    84.         return res == null ? "" : res;
    85.     }
    86.  
    87.     private boolean meetRequirementsOrNot(Map<Character, Integer> owesCharCountMap) {
    88.  
    89.         for (Integer v : owesCharCountMap.values()) {
    90.             if (v == null) {
    91.                 continue;
    92.             }
    93.             if (v > 0) {
    94.                 return false;
    95.             }
    96.         }
    97.         return true;
    98.     }
    99.  
    100.     private boolean isNecessary(int left, String s, Map<Character, Integer> owesCharCountMap) {
    101.         //left 位置的字符
    102.         char leftChar = s.charAt(left);
    103.         //当前亏欠map中的对应的亏欠数目
    104.         Integer count = owesCharCountMap.get(leftChar);
    105.  
    106.         //为null 说明这个字符都不是t字符串中的字符 那么说明left位置的字符没必要存在于窗口中
    107.         if (count == null) {
    108.             return false;
    109.         }
    110.  
    111.         //如果大于等于0 说明当前亏欠这个字符， 或者刚刚好，
    112.         //如果移动那么窗口中的字符数将不够覆盖t中所有字符
    113.         if (count >= 0) {
    114.             return true;
    115.         }
    116.  
    117.         //说明left处的字符不是必要的
    118.         //说明 当前窗口中这个字符的数量已经大于t中这个字符的数量
    119.         return false;
    120.     }
    121.  
    122. }

    三丶[串联所有单词的子串](30. 串联所有单词的子串 - 力扣（Leetcode）)#

    思路：#

    我的思路其实和第二题一样，也是恢复一个亏欠map 然后进行滑动窗口，只是这个开始滑动的位置应该是1~单个单词长度这个范围都进行滑动窗口，这一点很关键。

    然后我们需要处理两种情况

    • 滑动窗口中包含了 words中不存在的单词 ，那么前功尽弃，我们需要从这个不存在单词的结尾继续滑动
    • 滑动窗口中包含单词1的数量大于了words数组中单词1的数量，那么其实我们应该从第一个出现单词1位置的下一个位置开始滑动

    这个题推荐看题解30. 串联所有单词的子串 - 力扣（Leetcode）我的解法并不是很优秀

    代码：#

    1. class Solution {
    2.   public List<Integer> findSubstring(String s, String[] words) {
    3.  
    4.         List<Integer> res = new ArrayList<>();
    5.  
    6.         int singleWordLen = words[0].length();
    7.         if (singleWordLen * words.length > s.length()) {
    8.             return res;
    9.         }
    10.  
    11.       	//亏欠map
    12.         Map<String, Integer> owensMap = new HashMap<>();
    13.         for (String loop : words) {
    14.             owensMap.put(loop, owensMap.getOrDefault(loop, 0) + 1);
    15.         }
    16. 		
    17.         int roundStartPos = 0;
    18.       //从第一个位置开始 ，第二个位置开始 。。到单个单词长度个位置  
    19.       while (roundStartPos < singleWordLen) {
    20.             Map<String, Integer> owensMapTemp = new HashMap<>(owensMap);
    21.             int left = roundStartPos;
    22.             int right = roundStartPos;
    23.           
    24.             //滑动窗口
    25.             while (right <= s.length() - singleWordLen) {
    26.  
    27.                 //left 位置的单词 不是必要的
    28.                 while (left < right && !isNecessary(left, singleWordLen, s, owensMapTemp)) {
    29.                     String temp = s.substring(left, left + singleWordLen);
    30.                     Integer count = owensMapTemp.get(temp);
    31.                     if (count != null) {
    32.                         owensMapTemp.put(temp, count + 1);
    33.                     }
    34.                     left += singleWordLen;
    35.                 }
    36. 			
    37.                 //right位置的单词
    38.                 String rightString = s.substring(right, right + singleWordLen);
    39.                 Integer count = owensMapTemp.get(rightString);
    40.                 
    41.                 //right位置的单词 是我们需要的 那么维护亏欠map
    42.                 if (count != null && count >= 1) {
    43.                     owensMapTemp.put(rightString, count - 1);
    44.                     right += singleWordLen;
    45.                 } else {
    46.                     //right 位置的单词 不是words数组中的单词 那么直接然后right 跨过这个单词，直接从下一个单词开始
    47.                     if (count == null) {
    48.                         right = right + singleWordLen;
    49.                         left = right;
    50.                         owensMapTemp = new HashMap<>(owensMap);
    51.                     } else {
    52.                         //right位置的单词是words数组中的单词 但是当前窗口中这个单词数量 已经 大于words数组中这个单词数量的单词
    53.                         //那么删除头部的第一个单词 然后继续，
    54.                         String temp = s.substring(left, left + singleWordLen);
    55.                         Integer tempCount = owensMapTemp.get(temp);
    56.                         if (tempCount != null) {
    57.                             owensMapTemp.put(temp, tempCount + 1);
    58.                         }
    59.                         left += singleWordLen;
    60.                     }
    61.                 }
    62.  
    63.                 //符合要求 那么left 移动到下一个单词 并继续 找出所有答案
    64.                 if (meetRequire(owensMapTemp)) {
    65.                     res.add(left);
    66.                     String temp = s.substring(left, left + singleWordLen);
    67.                     Integer tempCount = owensMapTemp.get(temp);
    68.                     if (tempCount != null) {
    69.                         owensMapTemp.put(temp, tempCount + 1);
    70.                     }
    71.                     left += singleWordLen;
    72.                 }
    73.             }
    74.             roundStartPos++;
    75.         }
    76.         return res;
    77.     }
    78.  
    79.     private boolean isNecessary(int left, int singleWordLen, String s, Map<String, Integer> owensMapTemp) {
    80.         String temp = s.substring(left, left + singleWordLen);
    81.         Integer count = owensMapTemp.get(temp);
    82.         if (count == null) {
    83.             return false;
    84.         }
    85.         if (count < 0) {
    86.             return false;
    87.         }
    88.         return true;
    89.     }
    90.  
    91.     private boolean meetRequire(Map<String, Integer> owensMapTemp) {
    92.         for (Integer c : owensMapTemp.values()) {
    93.             if (c == null) {
    94.                 continue;
    95.             }
    96.             if (c > 0) {
    97.                 return false;
    98.             }
    99.         }
    100.         return true;
    101.     }
    102.  
    103. }

    四丶[重复的DNA序列](187. 重复的DNA序列 - 力扣（Leetcode）)#

    思路：#

    这个题挺逆天的，很难想到怎么用滑动窗口做，使用2进制表示字母A，C，G，T，分别使用00，01，02，03，这样窗口滑动的时候就是第一个字母出去，意味着二进制表示左移位2，右边字符进来，使用位操作

    代码：#

    1. class Solution {
    2.     public List<String> findRepeatedDnaSequences(String s) {
    3.         if(s == null || s.length()<=10){
    4.             return new ArrayList<>();
    5.         }
    6.  
    7.         List<String> res =  new LinkedList<>();
    8.         Map<Integer,Integer> memory = new  HashMap<Integer,Integer>();
    9.  
    10.         int right = 0;
    11.  
    12.         int firstBi = 0;
    13.         while(right<10){
    14.             firstBi = (firstBi<<2)| binaryOf(s.charAt(right));
    15.             right++;
    16.         }
    17.         memory.put(firstBi,1);
    18.         while(right < s.length()){
    19.             int bi = binaryOf(s.charAt(right));
    20.             //左边字符出去  右边字符进来
    21.             firstBi = ((firstBi<<2) |bi)&((1<<20)-1);;
    22.             int count =memory.getOrDefault(firstBi,0)+1;
    23.              memory.put(firstBi,count);
    24.             if(count == 2){
    25.                 res.add(s.substring(right+1-10,right+1));
    26.             }
    27.            
    28.             right++;
    29.         }
    30.         return res;
    31.     }
    32.  
    33.     private int binaryOf(char a){
    34.         if(a == 'A'){
    35.             return 0;
    36.         }
    37.          if(a == 'C'){
    38.             return 1;
    39.         }
    40.         if(a == 'G'){
    41.             return 2;
    42.         }
    43.          if(a == 'T'){
    44.             return 3;
    45.         }
    46.         return -1;
    47.     }
    48. }

    五丶[长度最小的子数组](209. 长度最小的子数组 - 力扣（Leetcode）)#

    思路：太简单了，窗口描述当前子数据，使用sum记录当前和，如果大于target那么更新长度，如果减去左边界的值还能大于，那么left++。直到right到 数组边界

    1. class Solution {
    2.    public int minSubArrayLen(int target, int[] nums) {
    3.         if(nums == null||nums.length == 0){
    4.             return 0;
    5.         }
    6.  
    7.         int left = 0;
    8.         int right = 1;
    9.         int sum =nums[0];
    10.         int minLen = sum>target?1:0;;
    11.         while(right<nums.length){
    12.  
    13.             sum +=nums[right];
    14.             
    15.             while(left<right && sum - nums[left]>=target){
    16.                 sum -= nums[left];
    17.                 left++;
    18.             }
    19.             
    20.             if(sum>=target){
    21.                 if(minLen == 0||minLen>right-left+1){
    22.                     minLen = right - left+1;
    23.                 }
    24.             }
    25.  
    26.             right++;
    27.         }
    28.         return minLen;
    29.  
    30.     }
    31. }

    六丶[存在重复元素 II](219. 存在重复元素 II - 力扣（Leetcode）)#

    思路：#

    维护一个长度为k的滑动窗口，使用set记录窗口中的数字，每次left位置的数据从窗口中出去，right位置的数进来，首先删除set中left代表的数字，然后如果right位置的数字存在于set中那么说明重复

    代码：#

    1.   public boolean containsNearbyDuplicate(int[] nums, int k) {
    2.         if(nums == null || nums.length<=1){
    3.             return false;
    4.         }
    5.         if(k == 0){
    6.             return false;
    7.         }
    8.         int left = 0;
    9.         int right = 0;
    10.         Set<Integer>memory = new HashSet<Integer>();
    11.  
    12.  
    13.         while(right<k+1 && right<nums.length){
    14.             if(!memory.add(nums[right])){
    15.                 return true;
    16.             }
    17.             right++;
    18.         }
    19.         
    20.         while(right <nums.length){
    21.             int newNum = nums[right];
    22.             memory.remove(nums[left++]);
    23.             right++;
    24.             if(!memory.add(newNum)){
    25.                 return true;
    26.             }
    27.         }
    28.         return false;
    29.     }

    七丶[存在重复元素 III](220. 存在重复元素 III - 力扣（Leetcode）)#

    思路：#

    思路和六类似，但是问题在于，我们如何快速的判断是否存在一个数，它和窗口中的数满足abs(nums[i] - nums[j]) <= t，这时候我们应该想到TreeSet，基于红黑树进行如此的判断的速度是logN

    代码：#

    1. class Solution {
    2.     public boolean containsNearbyAlmostDuplicate(int[] nums, int indexDiff, int valueDiff) {
    3.         if (nums == null || nums.length == 0) {
    4.             return false;
    5.         }
    6.         if (indexDiff == 0) {
    7.             return false;
    8.         }
    9.  
    10.         TreeSet<Integer> ts = new TreeSet<>();
    11.         int left = 0;
    12.         int right = 0;
    13.         while (right < indexDiff + 1 && right < nums.length) {
    14.             if (exist(ts,nums[right],valueDiff)){
    15.                 return true;
    16.             }
    17.             ts.add(nums[right]);
    18.             right++;
    19.         }
    20.  
    21.         while (right < nums.length) {
    22.             ts.remove(nums[left++]);
    23.             if (exist(ts,nums[right],valueDiff)){
    24.                 return true;
    25.             }
    26.             ts.add(nums[right++]);
    27.         }
    28.  
    29.         return false;
    30.     }
    31.  
    32.     private boolean exist(TreeSet<Integer> ts, int value, int diff) {
    33.         //Set中是否 存在一个数A 满足 abs(A-value)<=diff
    34.         //A>=value 最小的数 min 是否满足 min - value <= diff
    35.         //A<=value 最大的数max 是否满足 value - max<= diff
    36.         Integer min = ts.ceiling(value);
    37.         if (min != null && min - value <= diff) {
    38.             return true;
    39.         }
    40.         Integer max = ts.floor(value);
    41.         if(max!=null&&value - max<=diff){
    42.             return true;
    43.         }
    44.         return false;
    45.     }
    46.  
    47. }

    八丶[滑动窗口最大值](239. 滑动窗口最大值 - 力扣（Leetcode）)#

    思路：#

    窗口大小恒定为k大小，从头移动到尾巴，我们需要一种数据结构记录窗口此时的最大值，第一反应使用优先队列，入队时right位置的值，出队是left位置的值，但是这存在一个问题，如1,3,-1,3,2,2,k=3.当前窗口运动到1,【3,-1,3】,2,2 优先队列记录了3，-1紧接着left位置元素删除的时候会导致队列中只有一个1，随后right位置入队，队列维护了-1，2导致结构少了一个3。我们需要转变思想，队列每一个元素记录两个内容——值和对应的下标，当我们发生堆顶元素下标不在窗口中的时候进行删除。

    上面优先队列的使用是整个复杂度来到NLogN，其实还有另外一个数据结构可以实现这个功能，单调栈——我们维护一个单调递减的栈，当j

    代码：#

    1.优先队列#

    1.  public int[] maxSlidingWindow(int[] nums, int k) {
    2.         //优先队列 维护滑动窗口中的最大值
    3.      
    4.         if(nums == null || nums.length < k ){
    5.             return nums;
    6.         }
    7.  
    8.         int[]res = new int[nums.length - k +1]; 
    9.  
    10.         //优先使用值进行比较，值越大越在堆顶
    11.         //其次使用下标进行比较，下表越大越在堆顶，下标越大 活得越久
    12.         PriorityQueue<int[]> q = new PriorityQueue<>((i,j)->i[0]!=j[0]?j[0]-i[0]:j[1]-i[1]);
    13.         int right = 0;
    14.         while(right<k){
    15.             q.add(new int[]{nums[right],right});
    16.             right++;
    17.         }
    18.         res[0] = q.peek()[0];
    19.         int count = 1;
    20.         while(right<nums.length){
    21.             q.offer(new int[]{nums[right],right});
    22.             
    23.             while(q.peek()[1] <= right - k){
    24.                 q.poll();
    25.             }
    26.             right++;
    27.             res[count++]=q.peek()[0];
    28.         }
    29.         return res;
    30.     }

    2.单调栈#

    1.  public int[] maxSlidingWindow(int[] nums, int k) {
    2.         if(nums == null ){
    3.             return nums;
    4.         }
    5.         int[]res = new int[nums.length - k +1];
    6.  
    7.  
    8.         //队列中的值是下标 但是必须保证这些下标值是单调递减的
    9.         //当前 i<j nums[j]>=nums[i] 这时候num[i]对应下标 不需要维护了
    10.      	//说是单调栈其实是双向队列，因为我们需要看栈底元素
    11.         LinkedList<Integer> ll = new LinkedList<Integer>();
    12.         int right = 0;
    13.      	//初始化双端队列
    14.         while(right < k){
    15. 			//nums[ll.getLast()] <= nums[right]
    16.             //对应 1，2，3，4 k =3 初始化的时候 【1，2，3】4 这时候我们只需要维护3即可
    17.             while(!ll.isEmpty() && nums[ll.getLast()] <= nums[right]){
    18.                ll.removeLast();
    19.             }
    20.             ll.addLast(right);
    21.             right++;
    22.         }
    23.  
    24.         res[0] = nums[ll.getFirst()];
    25.         int count = 1;
    26.  
    27.         while(right < nums.length){
    28.           //同上
    29.            while(!ll.isEmpty() && nums[ll.getLast()] <= nums[right]){
    30.                 ll.removeLast();
    31.            }
    32.  
    33.            ll.addLast(right);
    34.            //如果队列头 也就是最大的值 将不处于窗口外
    35.            while(ll.getFirst() <= right-k){
    36.                ll.removeFirst();
    37.            }
    38.            res[count++] = nums[ll.getFirst()];
    39.            right++;
    40.         }
    41.  
    42.         return res;
    43.     }

    九丶[找到字符串中所有字母异位词](438. 找到字符串中所有字母异位词 - 力扣（Leetcode）)#

    思路：#

    滑动窗口大小为p长度，使用一个map记录窗口中字符和对应的数量，当每种字符数量和p相同是，记录下left的位置，left++的时候更新map，right++的时候更新map

    代码：#

    1. class Solution {
    2.     public List<Integer> findAnagrams(String s, String p) {
    3.         if(s == null || s.length()<p.length()){
    4.             return new ArrayList<>();
    5.         }
    6.         List<Integer> res = new ArrayList<>();
    7.         if(s.equals(p)){
    8.             res.add(0);
    9.             return res;
    10.         }
    11. 		
    12.         //记录p中的字符和对应的数量，因为都是小写字母，26长度的数组足以
    13.         int[] pCharCount = new int[26];
    14.         for(int i= 0; i<p.length();i++){
    15.             char c = p.charAt(i);
    16.             pCharCount[c-'a']++;
    17.         }
    18.  
    19.         //记录窗口中字符和队友的数量
    20.         int[] windowCharCount  = new int[26];
    21.         int left = 0 ;
    22.         int right = 0;
    23.         while(right<s.length()){
    24. 			
    25.             //左边界++
    26.             while(right - left + 1 > p.length()){
    27.                 windowCharCount[s.charAt(left)-'a']--;
    28.                 left++;
    29.             }
    30.  
    31.             //右边界++
    32.             windowCharCount[s.charAt(right)-'a']++;
    33.  
    34.             //字符和数目 和p一样
    35.             if(meetRequire(pCharCount,windowCharCount)){
    36.                 res.add(left);
    37.             }
    38.             right++;
    39.         }
    40.        return res;
    41.     }
    42.  
    43.     private boolean meetRequire(int[] pCharCount,int[] windowCharCount ){
    44.         for(int i =0;i<26;i++){
    45.             if(pCharCount[i]!=windowCharCount[i]){
    46.                 return false;
    47.             }
    48.         }
    49.         return true;
    50.     }
    51. }

    十丶[替换后的最长重复字符](424. 替换后的最长重复字符 - 力扣（Leetcode）)#

    思路：#

    维护一个窗口，我们需要保证窗口中的字符替换k次之后，都是相同的字符——字符总数-最大字符出现次数<=k

    如果不满足这个条件 那么左边界++，直到满足

    代码：#

    1. class Solution {
    2.     public int characterReplacement(String s, int k) {
    3.       if(s == null ){
    4.           return 0;
    5.       }
    6.  
    7.     if(s.length() <=k){
    8.         return s.length();
    9.     }
    10.     int res = 0;
    11.     int left = 0;
    12.     int right = 0;
    13.     int[]charCount = new int[26];
    14.  
    15.     while(right<s.length()){
    16.         charCount[s.charAt(right)-'A']++;
    17.         while(!meetRequire(charCount,k)){
    18.               charCount[s.charAt(left)-'A']--;
    19.             left++;
    20.  
    21.         }
    22.         res  = Math.max(res,right - left+1);
    23.         right++;
    24.     }
    25.     return res;
    26.  }
    27.  
    28.  
    29.  private boolean meetRequire(int[]charCount,int k){
    30.      int max = -1;
    31.      int sum = 0;
    32.      for(int c : charCount){
    33.          sum+=c;
    34.          max = Math.max(max,c);
    35.      }
    36.      return sum-max<=k;
    37.  }
    38. }
  • 相关阅读:
    redisson常用api
    项目经理如何做好跨部门沟通？
    如何使用JMeter操作Elasticsearch
    【MYSQL】表的增删改查
    Word2Vec
    2022-08-30 第五组 张明敏 学习笔记
    【MicroPython ESP32】通过sdcard模块读取SD卡实例
    交叉编译器arm-linux-gcc，aarch64-himix200-linux-gcc命令找不到 not found ，所有原因全方位解析
    FOC程序cubemx配置-ADC配置
    33岁程序员的年中总结
  • 原文地址：https://blog.csdn.net/jh035512/article/details/128109865