LeetCode - 76 最小覆盖子串

题目来源

76. 最小覆盖子串 - 力扣（LeetCode）

题目描述

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例

提示

• 1 <= s.length, t.length <= 10^5
• s 和 t 由英文字母组成

题目解析

本题要求的最小覆盖子串的含义是：包含某些指定字符，且要求最短的子串。

即题目要我们在s字符串中，找到一个子串，这个子串需要包含t字符串中所有字符，这样的子串有很多，我们需要其中最短的那个子串。

本题最容易想到的解法是滑动窗口，滑动窗口运动逻辑如下：

需要注意的是这里的滑动窗口是不定长的滑动窗口。

 以上就是变长滑动窗口的运动逻辑。

我们可以总结如下：

滑动窗口的范围即：左右指针的范围，初始时左右指针都指向索引0位置，

• 如果滑动窗口内部没有包含了t中所有字母，则右指针向右移动一格，然后继续判断滑动窗口内部是否包含了t中所有字母。
• 如果滑动窗口内部有包含了t中所有字母，（此时滑动窗口就是一个满足要求的子串，我们将他记录下来），则左指针向右移动一格，然后继续判断滑动窗口内部是否包含了t中所有字母。

按照上面逻辑，我们可以将记录的子串比较长度，保留最短的作为题解。

通过上面总结，我们似乎发现逻辑并不复杂，我们可以按照上面逻辑实现一下：

/**
 * @param {string} s
 * @param {string} t
 * @return {string}
 */
var minWindow = function (s, t) {
    if(s.length < t.length) return ''
 
    let l = 0
    let r = 0
 
    const ans = []
 
    while(r < s.length) {
        const subStr = s.substring(l,r+1)
        if(contain(subStr, t)) {
            ans.push(subStr)
            l++
        } else {
            r++
        }
    }
 
    if(!ans.length) return ''
 
    return ans.sort((a,b) => a.length - b.length)[0]
};
 
function contain(str, subStr) {
    const sup = {}
    for(let c of str) {
        sup[c] ? sup[c]++ : (sup[c]=1)
    }
 
    const sub = {}
    for(let c of subStr) {
        sub[c] ? sub[c]++ : (sub[c]=1)
    }
 
    let flag = true
    for(let c in sub) {
        if(!sup[c] || sub[c] > sup[c]) {
            flag = false
            break
        }
    }
 
    return flag
}

 但是结果却是超时，原因是我们算法的时间复杂度达到了O(n^2)，而数量级1 <= s.length, t.length <= 10^5，最终会有10^10次循环，这是肯定超时的。

我们可以看下上面的代码，找找那部分是可以优化的？

答案是contain函数，这个函数的作用是验证滑动窗口内部是否包含t字符串中所有字符的，但是方法比较笨，每当滑动窗口位置改变，就会重新统计字符数量，然后比较。这其中必然存在大量重复统计工作。

利用滑动窗口解决问题，我们一定要学会差集思想，因为滑动窗口的移动是有规律的，比如每次向右移动一格，这样本轮滑动窗口状态和上一轮滑动窗口状态，必然存在交集区域，如下图BC就是两次滑动窗口的交集区域

 交集区域我们是不需要关注的，只需关注差集区域，如上图A和D，本轮滑动窗口，相当于在上一轮滑动窗口的基础上，删除了一格A，增加了一格D，这样的话，统计本轮滑动窗口内容，就不需要O(n)时间，只需要O(1)时间了。

对于本题，滑动窗口的运动规律要复杂一点，并字符数量统计也不简单。

首先，我们需要统计字符串t中各字符的数量，比如t="ABC"，则统计结果为count: {A:1, B:1, C:1}，并记录总数量为len = t.length。

然后开始滑动窗口运动：

滑动窗口运动中新增的字符c（即右指针向右移动一格后新增的内容），如果在t中，即count[c]存在，则count[c]--，那么此时len要不要也自减呢？

我们看两种情况：

用例1：

s = "ADOBECODEBANC", t = "ABC"

情况1：

 此时右指针指向的字符A，在t中存在，因此count[c]--，count: {A:0, B:1, C:1}，此时应该len--，即len变为2。

情况2：

 此时右指针指向的字符“B”，在t中存在，因此count[c]--，count: {A:1, B:-1, C:0}，此时滑动窗口内部含有了两个B，但是这并不能意味着需要len也减去1，对于len来说，最多只能减去统计到B个数，如果B个数超出统计个数，即count[B] < 0，此时len不应该自减。

上面是右指针运动中的特殊情况处理，对应的还有左指针运动逻辑处理：

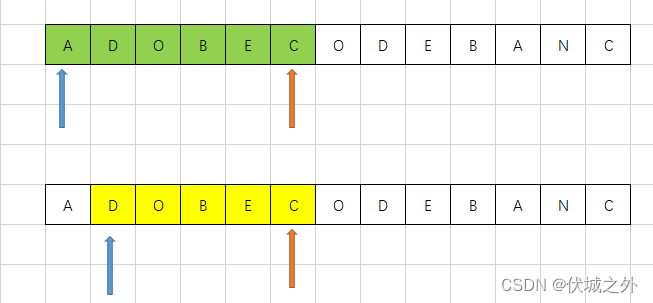
左指针运动，必然是找到了符合要求的子串，即滑动窗口内部含有了所有t字符，此时左指针右移一格，如上图，此时失去了A，而A刚好是t字符串内的字符，即count[A]存在，此时应该count[A]++，即将count:{A:0, B:0, C:0} 变为 count:{A:1, B:0, C:0}，而此时也应该len++。

但是对于

此时情况是，上面的滑窗的count: {A:0, B:-1, c:0}

当上面滑窗左指针右移一格后，变为下面的滑窗时，失去了B，刚好时t中字符，因此count[B]++，

此时 count: {A:0, B:0, c:0}，那么此时len是否也要自增1呢？答案是不需要，因为失去的B是超出统计个数的，因此失去了不需要作任何处理。

JS算法源码

/**
 * @param {string} s
 * @param {string} t
 * @return {string}
 */
var minWindow = function (s, t) {
  let len = t.length;
 
  const count = {};
  for (let c of t) {
    count[c] ? count[c]++ : (count[c] = 1);
  }
 
  let i = 0;
  let j = 0;
  let minLen = s.length + 1; // 最短子串的长度
  let start = 0; // 最短子串的起始位置
 
  while (j < s.length) {
    const jc = s[j];
 
    if (count[jc]-- > 0) { // 注意：这里count[c]--必须写在if条件中，因为count[jc]可以是负数，但是len不能是负数
      len--;
    }
 
    while (len === 0) {
      if (minLen > j - i + 1) {
        minLen = j - i + 1;
        start = i;
      }
 
      const ic = s[i];
      if (count[ic]++ == 0) { // 此时原因请看博客评论区说明
        len++;
      }
      i++;
    }
 
    j++;
  }
 
  return minLen < s.length + 1 ? s.substring(start, start + minLen) : "";
};

 

Python算法源码

class Solution(object):
    def minWindow(self, s, t):
        total = len(t)
 
        count = {}
        for c in t:
            if count.get(c) is None:
                count[c] = 0
            count[c] += 1
        
        i = 0
        j = 0
        minLen = len(s) + 1  # 最短子串的长度
        start = 0  #  最短子串的起始位置
 
        while j < len(s):
            jc = s[j]
 
            if count.get(jc) is not None:
                if count[jc] > 0:
                    total -= 1  # 注意：count[jc]可以是负数，但是total不能是负数
                count[jc] -= 1
                
            while total == 0:
                if minLen > j - i + 1:
                    minLen = j - i + 1
                    start = i
                
                ic = s[i]
                if count.get(ic) is not None:
                    if count[ic] == 0:  # 此时原因请看博客评论区说明
                        total += 1
                    count[ic] += 1
                i += 1
            
            j += 1
        
        return s[start:start+minLen] if minLen < len(s) + 1 else ""

 

Java算法源码

class Solution {
  public String minWindow(String s, String t) {
    int len = t.length();
 
    int[] count = new int[128];
 
    for(int i=0; i
      char c = t.charAt(i);
      count[c]++;
    }
 
    int i=0;
    int j=0;
    int minLen = s.length() + 1;
    int start = 0;
    while(j < s.length()) {
      char jc = s.charAt(j);
 
      if(count[jc]-- > 0) {
        len--;
      }
 
      while(len == 0) {
        if(minLen > j - i + 1) {
          minLen = j - i + 1;
          start = i;
        }
 
        char ic = s.charAt(i);
        if(count[ic]++ == 0) { // 此时原因请看博客评论区说明
          len++;
        }
        i++;
      }
      j++;
    }
 
    return minLen < s.length() + 1 ? s.substring(start, start+minLen) : "";
  }
}