力扣 112. 路径总和

力扣 112. 路径总和

题目

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。
1
2
3

示例 2：

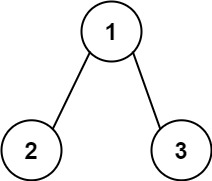
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
1
2
3
4
5
6

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。
1
2
3

提示：

• 树中节点的数目在范围 [0, 5000] 内
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

解

三种解法

• DFS 这个也算是一种递归
• BFS
• 递归

nm，真就万物皆可递归呗，递归大法好

emmm，现在是用的JS刷题，也是首次用JS写DFS、BFS，我感觉甚至比用C++写起来简单

DFS

• 时间复杂度 O(n)
• 空间复杂度 O(n)

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {boolean}
 */
var hasPathSum = function(root, targetSum) {
    if(!root) return false;
    let res = false;
    let dfs = (root, sum) => {
        if(sum == targetSum && !root.left && !root.right) res = true;
        if(root.left) dfs(root.left, sum + root.left.val);
        if(root.right) dfs(root.right, sum + root.right.val);
    }
    dfs(root, root.val);
    return res;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

BFS

• 时间复杂度 O(n)
• 空间复杂度 O(n)

这个就是用一个队列去维护遍历的结点，语法上用到了解构赋值也

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {boolean}
 */
var hasPathSum = function(root, targetSum) {
    // bfs
    if(!root) return false;
    const stack = [[root, root.val]]
    while(stack.length) {
        const [r,v] = stack.shift();
        if(v == targetSum && !r.left && !r.right) return true;
        if(r.left) stack.push([r.left, v + r.left.val]);
        if(r.right) stack.push([r.right, v + r.right.val]);
    }
    return false;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

递归

• 时间复杂度 O(n)
• 空间复杂度 O(n)

优雅，真的优雅

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {boolean}
 */
var hasPathSum = function(root, targetSum) {
    if(!root) {
        return false;
    }
    if(!root.left && !root.right) return root.val == targetSum;
    return (hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val));
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

仅供参考