【数据结构】栈

光荣与梦想千篇一律

自律和忍耐万里挑一

---

目录

1.栈的概念

2.栈的方法

3.模拟实现栈 

3.1 成员属性

3.2 构造方法

3.3 成员方法 

3.3.1 压栈 

3.3.2 出栈

3.3.3 异常 

3.3.4  查看元素

 3.3.5 清空栈

4.关于栈的 OJ 题 

4.1 有效的括号 （题目来源：力扣）

 4.2 逆波兰表达式求值（题目来源：力扣）

4.3 栈的压入、弹出序列

---

1.栈的概念

栈：一种特殊的线性表，栈只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除 操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out） 的原则。

进栈：将元素放入栈中称为进栈、入栈或压栈

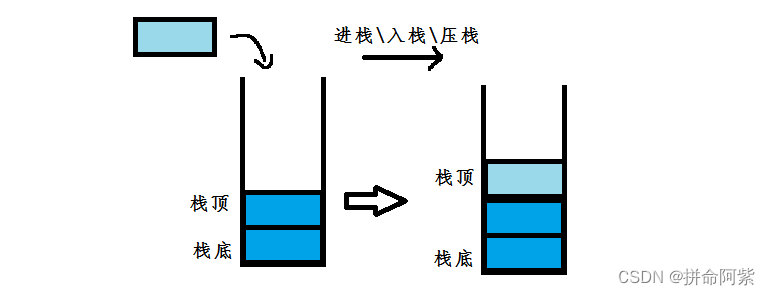
出栈：将元素从栈中删除称为出栈 

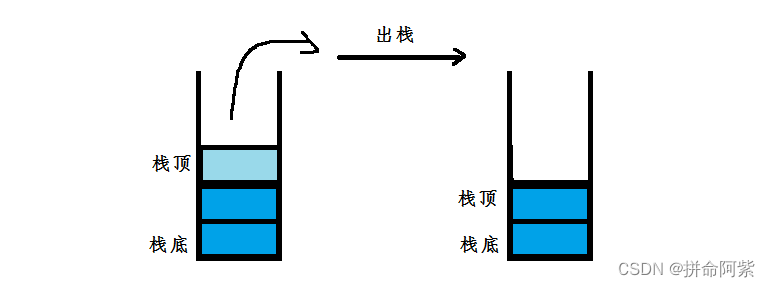
注：栈的所有操作都是在栈顶操作，因为栈遵循先进后出的原则 

2.栈的方法

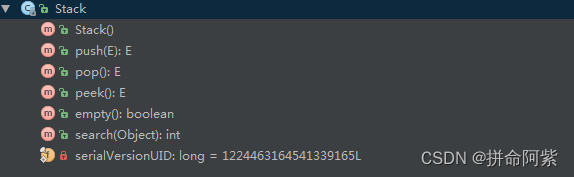
上述是在Java中的栈的方法，接下来我们就来看看上述常用方法的功能

3.模拟实现栈 

栈的所有操作只能在固定一端进行操作，所以它可以采取数组和链表进行存储

采用数组进行存储：可以在尾部进行插入和删除操作，这样时间复杂度为O(1)，但是美中不足点就是需要考虑扩容  

采用单链表进行存储：插入操作时间复杂度为O(1)，删除操作时间复杂度为O(n) 

采用双链表进行存储：插入和删除操作时间复杂度为O(1)，但是需要存储上一个节点的地址和下一个节点的地址

从时间复杂度和空间复杂度的角度，数组实现栈更好一点。并且Java内部也是用数组实现的存储栈 

那接下来我们就用数组实现栈： 

首先我们得写一个类，将栈的实现过程，成员方法成员属性全部放在这个类中：

public class MyStack {
 
}

3.1 成员属性

定义一个 elem 的数组用来存放数据 ，在定义一个整型变量 size 记录有效元素的个数。栈的所有操作都是在一端进行的，我们可以通过 size -1 找到最后一个元素的位置

private int[] elem; //存放数据的数组
private int size; //有效元素个数
private static final int DEFAULT_CAPACITY = 10; //约定好的默认容量

3.2 构造方法

每一次实例化 MyStack 这个类时，都会自动调用这个构造方法，这个构造方法会给 elem 数组开辟 DEFAULT_CAPACITY （10）个空间，构造方法在对象的运行期间只会执行一次

public MyStack() {
    this.elem = new int[DEFAULT_CAPACITY];
    this.size = 0;
}

3.3 成员方法 

3.3.1 压栈 

首先得判断数组容量是否已满，如果满了则需要扩容，扩容为有效元素个数的两倍，如果没满则不需要扩容。直接在数组的 size 位置添加元素，然后 size++ 。因为 size 是有效元素的个数，数组下标是从 0 开始，size - 1 则为最后一个元素，size 则为最后一个元素后面的一个位置

public int push(int data) {
    // 判断是否需要增容
    if (this.size == this.elem.length) {
        this.elem = Arrays.copyOf(this.elem, this.size * 2);
    }
    // 压栈只能往栈顶压栈
    this.elem[this.size++] = data;
    return data;
}

3.3.2 出栈

首先判断栈是否为 null，如果为空则不能出栈，直接报异常。如果不为空让 size = size - 1，因为出栈了一个元素，那么有效元素个数也就需要减少一个

// 出栈
public int pop() {
    // 判断栈是否为null
    if (this.size == 0) {
        throw new MyStackEmptyException("栈为空！");
    }
    this.size = this.size - 1;
    return this.elem[this.size];
}

3.3.3 异常 

public class MyStackEmptyException extends RuntimeException {
    public MyStackEmptyException() {
    }
 
    public MyStackEmptyException(String message) {
        super(message);
    }
}

3.3.4  查看元素

首先判断栈是否为 null，如果为空则不能出栈，直接报异常。如果不为空则直接返回最后一个元素

// 查看栈顶元素
public int peek() {
    // 判断栈是否为null
    if (this.size == 0) {
        throw new MyStackEmptyException("栈为空！");
    }
    return this.elem[this.size - 1];
}

 3.3.5 清空栈

直接让 size = 0 

public boolean empty() {
    return this.size == 0;
}

4.关于栈的 OJ 题 

4.1 有效的括号 （题目来源：力扣）

题目：给定一个只包括 '( '，')'，'{'，'}'，'['，']' 的字符串 s ,判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

解题思路：如果字符串为空，则返回 false。否则就实例化一个栈，依次遍历字符串中的每一个字符，如果为左括号，则直接入栈。如果为右括号，则先判断栈是否为空，如果为空则说明右括号没有对应的左括号，则直接返回false。如果栈不为空，则出栈顶的元素，并且将这个元素的值用一个临时变量存储起来，然后判断这两个括号是否匹配，如果不匹配则直接返回false。如果匹配则继续执行字符串下一个字符，直到遍历完字符串中的每一个字符，才会跳出循环。跳出循环后，判断栈是否为空，如果为空，说明括号全部匹配。如果不为空，说明左括号比右括号多则返回 false。

import java.util.*;
class Solution {
    public boolean isValid(String s) {
        //判断字符串是否为空
        if(s == null) {
            return false;
        }
        //实例化一个栈
        Stack stack = new Stack<>();
        //遍历字符串中的每一个字符
        for(int i = 0; i < s.length(); i++) {
            char right = s.charAt(i);//获取字符串中第i个位置的字符
            //判断字符串是否为左括号
            if(right == '(' || right == '{' || right == '[') {
                stack.push(right);//入栈
            } else {
                //判断栈是否为空
                if(stack.empty()) {
                    return false;
                } else {
                    char left = stack.pop();//出栈
                    //判断左括号与右括号是否匹配
                    if(!(left == '(' && right == ')' || left == '{' && right == '}' || left == '[' && right == ']')) {
                        return false;
                    }
                }
            }
        }
        if(stack.empty()) {
            return true;
        }
        return false;
    }
}

 4.2 逆波兰表达式求值（题目来源：力扣）

题目：根据逆波兰表示法，求表达式的值。

有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

注意 两个整数之间的除法只保留整数部分。

可以保证给定的逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

解题思路：首先判断这个字符串数组是否为空，如果为空我们就返回一个无效的值（假设这个无效的值为：-1），那我们就返回 -1。如果不为空我们就创建一个存储整型元素的栈，用来存储左操作数和右操作数。然后我们就遍历字符串数组，每一次遍历的时候我们都需要判断它是否为 + - * / 这些操作符，如果不是就将这个字符串转换为整型数入栈，如果是则需要判断栈当中是否有两个及以上的操作数，如果有则需要在栈中pop两个元素并存储在两个整型变量中当做左操作数和右操作数，然后匹配对应的操作符进行运算将运行的结果在放入栈中，如果栈中小于两个元素则返回无效值。如果在循环的时候没有返回，说明运算完成，将栈中最后一个元素pop并且返回即可。

class Solution {
    public int evalRPN(String[] tokens) {
        if (tokens == null) {
            return -1;
        }
        Stack stack = new Stack<>();
        for (int i = 0; i < tokens.length; i++) {
            if (!(tokens[i].equals("+") || tokens[i].equals("-") || tokens[i].equals("*")  || tokens[i].equals("/"))) {
                int tmp = Integer.parseInt(tokens[i]);
                stack.push(tmp);
            } else if (stack.size() >= 2){
                int right = stack.pop();
                int left = stack.pop();
                int sum = 0;
                switch (tokens[i]) {
                    case "+":sum = left + right;break;
                    case "-":sum = left - right;break;
                    case "*":sum = left * right;break;
                    case "/":sum = left / right;break;
                }
                stack.push(sum);
 
            } else {
                return -1;
            }
        }
        return stack.pop();
    }
}

4.3 栈的压入、弹出序列

题目：输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。 

解题思路：首先判断传过来的两个整型数组是否都为空，如果都为空则返回 true。否则判断它们两个当中是否有一个为空，如果有则返回 false。否则就判断两个数组的长度是否相同，如果不相同则直接返回 false。然后上述的条件都不满足则说明数组都不为空，且长度相等。创建一个存放整型元素的栈，创建两个整型变量i，j用来存放两个数组的下标位置。然后遍历 pushA 数组，在遍历的时候判断 pushA[i] 位置的元素是否与 popA[j] 位置的元素不相等，如果不相等则把 pushA[i] 位置的元素入栈，如果相等则不让 pushA[i] 位置的元素入栈，然后 j++，循环判断栈是否为空且判断栈顶元素与此时的 popA[j] 是否相等，如果不为空且栈顶元素与此时的 popA[j] 相等，则出栈，然后j++。当遍历完 pushA 时，判断栈是否为空，如果为空则返回 true，否则返回 false。

import java.util.*;
public class Solution {
    public boolean IsPopOrder(int [] pushA,int [] popA) {
        if(pushA == null && popA == null) {
            return true;
        } else if(pushA == null || popA == null) {
            return false;
        } else if(pushA.length != popA.length) {
            return false;
        }
        Stack stack = new Stack<>();
        int i = 0;
        int j = 0;
        while(i < pushA.length) {
            if(pushA[i] != popA[j]) {
                stack.push(pushA[i]);
            } else {
                j++;
                while(!(stack.empty()) && stack.peek() == popA[j]) {
                    stack.pop();
                    j++;
                }
            }
            i++;
        }
        if(stack.empty()) {
            return true;
        }
        return false;
    }
}