泊松随机变量的分解与求和

1.泊松随机变量的分解

假设传感器发出的信号为0-1信号.发出1的概率为,发出0的概率为 ,并且和以前所发的信号独立.现在假设一定时间内发出信号的个数为泊松随机变量，其参数为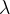, 可以证明在同一段时间内发出1的个数也是泊松随机变量，其参数为.

证明：设 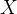和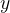分别为同一时间段内发出的信号1和0的个数，那么就是这一时间段内发出信号的个数，利用全概率公式，得到

        \(\begin{align} P(X=n,Y=m) &=P(X=n,Y=m|Z=n+m)P(Z=n+m) \nonumber \\ &=\binom{n+m}{n}p^n(1-p)^m\cdot \frac{e^{-\lambda}\lambda^{n+m}}{(n+m)!} \nonumber \\ &=\frac{e^{-\lambda p}(\lambda p)^n}{n!}\cdot \frac{e^{-\lambda(1-p)}\(\lambda(1-p))^{m}}{m!} \nonumber \end{align}\)

由此得到

                \(\begin{align} P(X=n) &=\sum_{m=0}^{\infty}P(X=n,Y=m) \nonumber \\ &=\frac{e^{ -\lambda p}(\lambda p)^n}{n!}e^{ -\lambda (1-p)}\sum_{m=0}^{\infty}\frac{((\lambda (1-p))^m}{m!} \nonumber \\ & =\frac{e^{ -\lambda p}(\lambda p)^n}{n!}e^{ -\lambda (1-p)}e^{ \lambda (1-p)} \nonumber \\ & = \frac{e^{ -\lambda p}(\lambda p)^n}{n!} \nonumber \end{align}\)

这说明 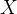是一个泊松随机变量，参数为.

2.独立泊松随机变量之和

设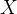和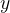为两个独立的泊松随机变量，均值分别为 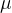和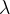，根据矩母函数的定义可知

                                ,                ​​​​​​​

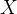计，由于 与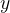相互独立，所以有：

        

上述矩母函数与均值为 的泊松随机变量的矩母函数相同.根据矩母函数的唯一性可知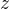，服从均值为​​​​​​​的泊松分布.