矩阵论复习提纲

矩阵论复习提纲

注意：只适合 CUIT 电子信息类研究生的 李胜坤 老师的矩阵理论复习

复习：逆矩阵求逆公式

第一章 矩阵相似变化

1、特征值与特征向量

• 定义：
  A ∈ C^nxn 若存在 λ ∈ C 满足 Ax = λx 则 λ 为 A 的特征值
  可转换为 （λI - A）x = 0
  特征多项式 ：det(λI - A)
  特征矩阵： λI - A

例题：

2、相似对角化

1.定义及性质

例题：

2. 判断可对角化&求相似变换矩阵

3. 计算相似对角化矩阵

3、Jordan标准形

J_i 除开主对角线上有只，其上对角线上的元素只能是1或0

1. 求Jordan标准形（线性法-只限于3阶）

2. 求非可对角化但可Jordan标准化的矩阵的相似变换矩阵

• 例1

• 例2

4、Schmidt 正交化

• 例题：
  

第二章 范数理论

1、向量范数

1. 范数计算

• ||x||₁ 范数
  

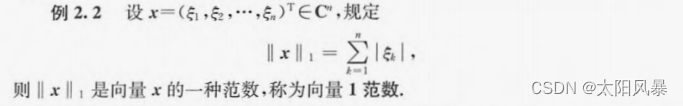
• ||x||₂ 范数
  

• ||x||_∞ 范数
  

例题：

2. 范数证明

• 证明模板：
  

例题：

2、矩阵范数

下面是矩阵范数的说明，没特别指明，矩阵就是方阵

1. 范数计算

• ||A||_m1 范数
  
• ||A||_F 范数
  
• ||A||_m∞ 范数
  
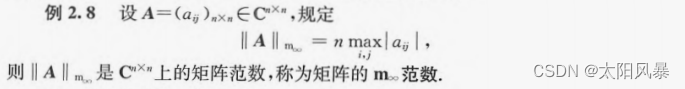
  其他矩阵范数
• ||A||₁ 范数、||A||₂ 范数、||A||_∞ 范数
  
  下面是长方阵的范数总结：
  

例题：

2. 范数证明

• 证明模板
  

例题：

第三章 矩阵分析

1、矩阵序列

• 可以利用矩阵范数来研究矩阵序列的极限
  设 A ∈ C^nxn，则A为收敛矩阵的充分必要条件是 ρ（A）< 1
  ρ（A）是A的某一矩阵范数
  推论： 设 A ∈ C^nxn 若对 C^nxn 上的某一矩阵范数 ||·|| 有 ||A||，则A为收敛矩阵.

例题：

第（1）题使用的是判别 ||A||₂ = （5/6）^(1/2) < 1
第（2）题使用的是判别 ||A||₁ = max{0.8, 0.9, 0.8} < 1

例题：

2、矩阵级数

1、矩阵级数

• 定义：
  

例题：

2、矩阵幂级数

定义：

例题：

3、矩阵函数

1. 利用Hamilton-Cayley定理

例题：

例题 3.5 这个能对角化的矩阵也可以用对角化来做，我也验证过了的，因为里面涉及到 i 虚数，就需要使用到欧拉公式

2. 利用 相似对角化

例题：

3. 利用Jordan 标准形

r_i : 是 重根的个数

例题：

例题：

4、矩阵微分积分

矩阵微积分其实都是对矩阵中每一项的微积分

1. 矩阵微分

性质：

例题·：

2. 矩阵积分

例题：

第四章 矩阵分解

1、矩阵的三角分解

1. Doolittle 分解 和 Crout 分解

例题：

2. Cholesky 分解

例题：

2、矩阵的QR分解

1. Household 矩阵

定义：

例题：

这里的 x^H 是共轭转置 ，其值就是 （2i, -i, 2）， ax^He₁ = 2ia

2. 矩阵QR分解（应该只考3阶）

定义：

这个最好看例题

1.HouseHolder变换

2. Schmidt 变化

• 定义：
  

• 例题:
  

3、矩阵的满秩分解

1. hermite 标准型 H 和 变换矩阵 S

例题：

2.满秩分解

定义：

例题：
这里的 j₁ , j₂ 的个数对应 H 的秩大小， j₁ , j₂ 的值对应 H 的最大线性无关组 向量位置
H 的 线性无关向量是 （1,0,0）^T, **（0,1,0）^T, ** 位置分别是 1，3 列

第五章 特征值的估计和表示

1、特征值界估计（估计不考）

2、Gerschgorin定理

定义：

• 简述：（行盖尔圆）
  圆中心：主对角线元素
  圆半径：去除对角线的行元素的绝对值之和

• 简述：（列盖尔圆）
  圆中心：主对角线元素
  圆半径：去除对角线的列元素的绝对值之和

例题

2. 特征值隔离

例题：


在证明这个盖尔圆相关的证明题的时候，记住，

• 一个单独的盖尔圆就能有一个特征值
• 实特征值总是可以单独出现
• 复特征值必须是两个出现

课后例题：

3、广义特征值问题

定义：

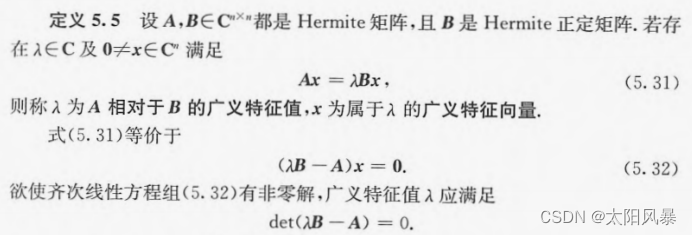
例题：

第六章 广义逆矩阵

1、Moore-Penrose 逆A⁺ 计算

定义：

例题：

2、A⁺在解线性方程组中的应用

结论：

为了方便理解：

一个判断条件，两个计算式，4个名称

例题：


觉得不错的，可以点个赞哦~