【LADRC】线性自抗扰控制

目录

综述文献学习

扰动响应

干扰观测器

LADRC算法

LADRC算法推导二阶线性系统为例

LADRC算法n阶

LADRC离散化—零阶保持法

一阶系统

二阶系统

LADRC参数整定方法

参考文献

---

综述文献学习

依靠模型建立控制律的方法，鲁棒性是个大问题，像机器人控制系统这种复杂的控制系统，会遇到“模型灾难”。

控制系统中，由于外输入和反馈的存在，线性和非线性并没有分明的界限。

控制的目的是对一个“过程”的某种优化，并不是“全局”控制。

不管线性还是非线性系统，在一定条件下都可以通过反馈转换为线性积分器串联形式，称为反馈系统的基本结构。它的意义是不管原始系统物理性质是什么，是线性还是非线性，最后都可以通过反馈还原到最简单、最基本、最原始和最理想的形式，即积分器串联型。

线性系统理论定的标准型，可控型、可观型、Jordan标准型、横山标准型等都适用于开环系统。

外扰指系统外部环境中带来的未知摄动，内扰指系统的未知动态和它的变化，总扰动指外扰加内扰。

积分器的作用是在稳态估计总扰动，但是积分器相位滞后，在瞬态影响控制效果，甚至造成系统的不稳定。

PID和ADRC的区别在于，PID利用积分项给系统升阶，估计和补偿总扰动；ADRC克服了积分器的缺点，对总扰动进行全程估计和补偿。

一个控制系统要使输出迅速跟踪给定值有两个途径：高带宽和前馈。但是工业上带宽就是成本，高带宽虽然能使跟踪速度提高，但是也存在一些问题：

1. 对执行机构的品质要求提高；
2. 激励了对象的高频动态使控制问题复杂化；
3. 闭环系统的稳定裕度下降；
4. 对传感器噪声更敏感。

控制系统和滤波系统的根本不同：

1. 被控对象不像滤波器，不可轻易改变；
2. 被控对象中存在各种不同的扰动；
3. 被控对象中的各种机械环节包括液压、气压动力系统的不确定性远远大于滤波器的参数变化；
4. 被控系统的设计要求与滤波远远不同，特别是不允许输出的滞后。

信息的选择、提取、品质和使用等问题是控制工程特有的问题，也是控制论要研究的本质问题。

《工程控制论》中有三个观点令人深思：

1. 基于传递函数的设计方法过于复杂，不适合工程实际的需要；
2. 被控对象不仅有外扰还有内扰，工程控制的基本问题是要使系统能够在扰动影响下稳定运行；
3. 控制器设计要摆脱对模型的依赖，依靠的是在恶劣的工作环境中对系统持续的测量和感知。

控制器要实时的提取在线信息而不能依赖模型信息。

指南车的发明说明，自动控制并非一定要依赖被控量的反馈信息，它也可以通过扰动信息的反馈实现。

前馈信息的本质：用离线信息弥补在线信息的不足。

抗扰可以在扰动还没有来得及对输出产生很大影响之前完成。

扰动响应

扰动一般施加在被控对象之前，并且扰动只能在引起输出发生偏移之后才能被检测出来，所以控制系统无法完全消除扰动。典型的扰动响应，由于有电容器，在高频段扰动响应表现好，由于有积分器，在扰动响应表现好，但是在中频段，扰动响应表现差。

扰动响应T(s)定义为系统输出C(s)对扰动输入D(s)的响应，理想扰动响应为负无穷dB，即T(s)=0。

从扰动响应传递函数可以看出，改善扰动响应，可以采用响应缓慢的被控对象，也可以通过增大控制器增益。

响应缓慢的被控对象，如大惯量器件或大电容，但是会增加成本。

增大控制器增益，包括增加比例增益和积分增益，增加比例增益既可以改善指令响应，也可以改善扰动响应（优化高频分量扰动）；增加积分增益，对于指令响应改善有限，但是可以改善扰动响应（优化低频分量扰动）。

由于系统存在稳定性要求，稳定裕度小的系统，不能无限制的增加控制器增益。此时，对扰动进行测量或估计，在功率变换器之前减去等效的扰动量，近似消除扰动，这种方法称为扰动解耦法，比如自抗扰控制中的扩张状态观测器。

在系统稳定的前提下，增大控制器增益配合扰动解耦法，可以有效改善扰动响应。

干扰观测器

大多数情况下，干扰信息并不能准确的获知与测量（如实加负载、未知扰动等），必须依据模型信息和在线输入输出数据对干扰进行观测，然后基于干扰观测器计算相应的控制值，实现对干扰的直接补偿或抑制干扰带来的不利影响。

干扰观测器可以作为单独或附加模块存在于控制系统中，系统中原有的控制器用来实现最优跟踪性能，当不存在扰动或扰动可以忽略不计时，干扰观测器没有输出，对控制系统没有影响。

实际应用应综合使用：前馈 + 干扰观测器 + 反馈

干扰观测器又分为基于准确对象模型和不需要准确对象模型，其中不需要准确对象模型的有ADRC中的ESO（自抗扰控制中扩张状态观测器），只需要知道系统相对阶数和输入，ESO观测系统的总扰动（未建模动态、外部干扰和参数变化都归为总扰动）

LADRC算法

自抗扰控制（ADRC，Active Disturbance Rejection Control）是由韩京清先生提出的一种不依赖对象模型的控制算法，针对ADRC参数整定困难问题，高志强教授提出线性自抗扰控制（LADRC），将ADRC参数与控制器和观测器的频率联系起来，把参数整定问题转化为带宽调节问题。

  LADRC基本结构图

自抗扰控制的精髓：扰动估计和补偿。

总扰动 =内部扰动 （系统模型的不确定性）+ 外部扰动

线性扩张状态观测器LESO可分为无对象模型线性扩张状态观测器、模型辅助线性扩张状态观测器和降阶线性扩张状态观测器。

线性误差反馈控制律LSEF中存在补偿分量对总扰动进行实时估计和补偿。

使用LESO对总扰动进行估计，使用LSEF消除总扰动

LADRC算法推导二阶线性系统为例

 y为输出，u为输入，x1、x2和x3为状态变量，x3为扩张状态（状态变量数=系统阶数，二阶系统所以x3成为扩张状态），w为扰动，f为总扰动，扩张状态空间方程：

无对象模型线性扩张状态观测器：

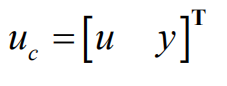
 其中，yc为输出，z为观测器的状态向量，L为观测器误差反馈增益矩阵。

  由下式

观测器增益矩阵L与观测器带宽w0：

 线性误差反馈控制律：

其中，u0： 

r为给定值，z1、z2和z3为观测器状态， kp和kd是控制器的增益。

控制器带宽：

   综上可得线性自抗扰控制算法公式：

LADRC算法n阶

 总扰动f扩张成第n+1个状态变量

 

观测器带宽w0：决定了观测器的跟踪速度，w0越大，观测器估计精度越高，抗干扰能力越强，瞬态响应速度加快，但是w0过大，会引入高频噪声，系统不稳定。w0参数应该考虑估计性能和噪声容许量。 

控制器带宽wc：决定了控制器的响应速度，wc越大，系统响应速度越快，但是wc过大会导致系统超调甚至不稳定。过大会引入更多噪声，所以满足控制性能时，应选择较小的wc。

扰动补偿b0：表示控制对象的特性，可以由阶跃对象的初始加速度导出，b0越大，抗干扰能力越弱，为了使系统保持稳定，b0不能过大也不能过小。

w0和wc的关系：近似有w0=（2~10）wc或w0=（3~5）wc一般取w0=4wc。

LADRC离散化—零阶保持法

LADRC算法在计算机上运行需要离散化，在固定采样率下运行。控制器部分值针对观测器输出分别按照kp、kd放大组合，不需要离散，只需要对观测器进行离散化。

当前零阶保持法效果优于当前一阶保持法和当前欧拉法，形式上更简单，相位滞后更小。零阶保持法在被离散对象前加零阶保持器，然后一起z变换离散化。

离散估计器极点与连续观测期极点之间的关系如下，其中h为采样周期。

一阶系统

一阶系统连续模型：

 省略f， 添加零阶保持器后z变换得：

 离散估计器方程如下，其中ud(k)为离散估计器输入组合，yd(k)为离散估计器输出，Lc为离散估计器误差反馈增益矩阵。

使下式成立， 

 得到离散估计器误差反馈增益矩阵：

  最终得到一阶系统离散估计器方程：

二阶系统

二阶系统连续模型：

省略f， 添加零阶保持器后z变换得：

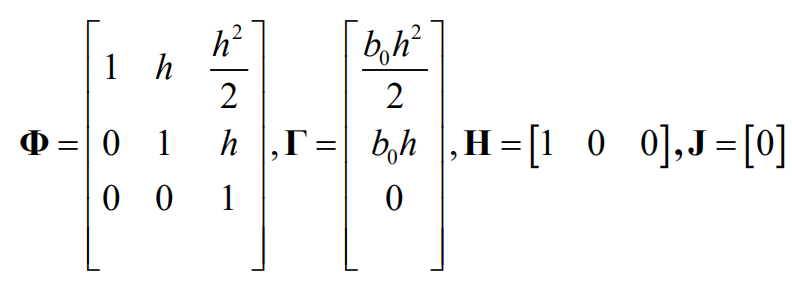
离散估计器方程如下，其中ud(k)为离散估计器输入组合，yd(k)为离散估计器输出，Lc为离散估计器误差反馈增益矩阵。

使下式成立，

得到离散估计器误差反馈增益矩阵：

 最终得到二阶系统离散估计器方程：

LADRC参数整定方法

1.设置一个较小的b0，使系统运行，逐渐增大b0，直到控制效果相对稳定。

2.设置较小的wc，较大的w0。

2.逐渐增大wc，期间如果系统不稳定，观察系统是否发生抖动，则重新增大b0。

参考文献

[1]韩京清.控制理论——模型论还是控制论[J].系统科学与数学,1989,(04):328-335.

[2]高志强 (2013). 重读《控制理论---模型论还是控制论》有感.

[3]高志强.自抗扰控制思想探究[J].控制理论与应用,2013,30(12):1498-1510.

[4]高志强.浅谈工程控制的信息问题[J].系统科学与数学,2016,36(07):908-923.

[5]王传榜,王永,梁青.降阶自抗扰控制器对时滞系统控制研究[J].控制工程,2016,23(10):1602-1606.DOI:10.14107/j.cnki.kzgc.140569.

[6]梁青,王传榜,潘金文,卫一恒,王永.线性自抗扰控制参数b_0辨识及参数整定规律[J].控制与决策,2015,30(09):1691-1695.DOI:10.13195/j.kzyjc.2014.0943.

[7]朱斌.自抗扰控制入门

[8]George Ellis. Control System Design Guide.