[dp]洛谷P1990 覆盖墙壁 / Leecode790. 多米诺和托米诺平铺

洛谷题目链接
Leecode题目链接

这两道题本质上是同一道题.在洛谷挺早就见过这道题了,但由于过于抽象没看懂就没做,直到今天在Leecode每日一题又见到了这道题.

看到大概就能猜出来用dp来做,因为满足了使用dp的无后效性(后面作出的操作不影响已经做完操作的结果)和子问题重叠(每铺一块砖都可以看作是一个子问题).而题目要求给出所有方案,不分优劣只数数量.最大的问题还是状态转移方程怎么写.

按力扣官方题解的思路来说一下这道题.按列从1到n枚举每一列,确保这一列之前没有未上色的方块,这一列之后没有已上色的方块.

此时我们枚举的这一列有四种可能的情况:

1. 两个方块都未被上色
2. 上方的方块被上色,下方的方块未被上色
3. 下方的方块被上色,上方的方块未被上色
4. 两个方块均被上色

四种情况的示意图如下,右边一列为枚举下标所在列

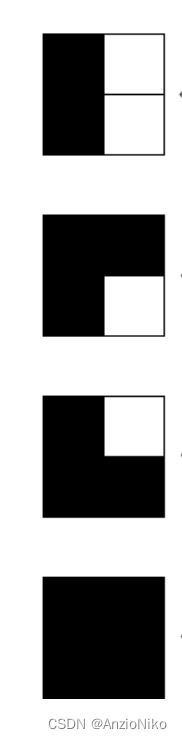
将这四种状态命名为0,1,2,3,用$dp[i][x]$表示第i列出现x情况的方法数量,可知在枚举结束后第n列第三种状态的方法数即$dp[n][3]$为答案.

接下来讨论在这四种状态如何由前方的状态转移过来.

对于$d[i][0]$状态,它和$dp[i-1][3]$状态是完全相同的,所以直接赋值.

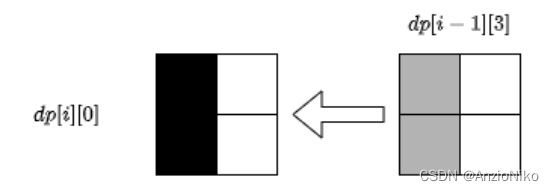
对于$d[i][1]$状态,可以由$dp[i-1][0]$接上一个L形方块转移,也可以由$dp[i-1][2]$接上一个长条形方块转移.

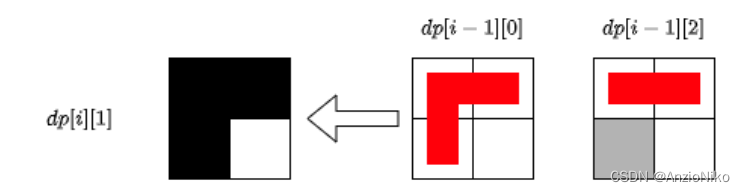
对于$d[i][2]$状态,相当于$d[i][1]$状态的镜像,可以由$dp[i-1][0]$接上一个L形方块转移,也可以由$dp[i-1][1]$接上一个长条形方块转移.

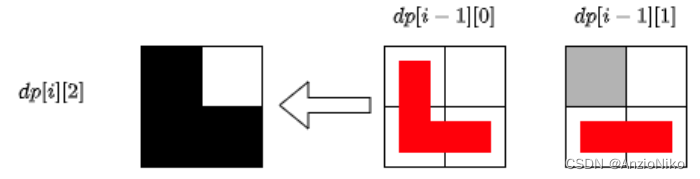
而对于$d[i][3]$状态,可以由$d[i-1][0]$加两个横向长条方块转移,也可以由$d[i-1][1]$和$d[i-1][2]$加上一个L形方块转移,还可以由$d[i-1][3]$加上一个纵向长条方块转移.

将$dp[0][0],dp[0][1],dp[0][2]$赋初值0,$dp[0][3]$赋初值1,即可进行状态转移.

过程中需要注意数据量过大导致的溢出问题.Leecode要求对1e9+7取模,这就导致3状态的状态转移过程中就可能发生数据溢出,所以要对每一次两两相加的运算进行取余,防止溢出.

class Solution {
	public int numTilings(int n) {
		int[][] dp = new int[n + 1][4];
		final int mod = (int) 1e9 + 7;
		/*
		一个正方形都没有被覆盖，记为状态 0；
		只有上方的正方形被覆盖，记为状态 1；
		只有下方的正方形被覆盖，记为状态 2；
		上下两个正方形都被覆盖，记为状态 3。
		 */
		dp[0][3] = 1;
		for (int i = 1; i <= n; i++) {
			dp[i][0] = dp[i - 1][3];
			dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % mod;
			dp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % mod;
			dp[i][3] = (((dp[i - 1][0] + dp[i - 1][1]) % mod + dp[i - 1][2]) % mod + dp[i - 1][3]) % mod;
		}
		
		return dp[n][3];
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21