1143 汉诺塔

题目描述

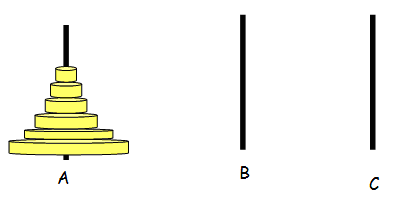
汉诺塔问题是这样的：有3根柱子A,B,C，其中A柱上有64个盘子，盘子大小不等，大的在下，小的在上。要求把这64个盘子从A柱移到C柱上，在移动过程中可以借助B柱，每次只允许移动一个盘子，且在移动过程中在三根柱子上都保持大盘在下，小盘在上。从键盘输入一个整数n(n<=64)表示盘子的个数，打印出移动盘子的正确步骤。

输入要求

从键盘输入盘子的个数n。

输出要求

打印出n个盘子的移动步骤。每一步骤占据一行。

输入样例

3

输出样例

a->c
a->b
c->b
a->c
b->a
b->c
a->c

在这里我们运用了递归的思想 

可以先看看找规律

当n=1时：移动1 方向 A—>C; 

当n=2时：移动1 方向 A—>B;
移动2 方向 A—>C;
移动1 方向 B—>C; 

当n=3时：移动1 方向 A—>C;
移动2 方向 A—>B;
移动1 方向 C—>B;
移动3 方向 A—>C;
移动1 方向 B—>A;
移动2 方向 B—>C;
移动1 方向 A—>C; 

那么现在我们可以分为三步

1、把n-1个移到B（移动到B以后也是大圆盘的在下面，下同）

2、把第n个移到C

3、把n-1个从B移到C

现在我们把步奏细分

1、n-1个怎么移动到B呢（借助C柱）

2、将n-2个从A移动到C（我们会发现

现在是小的圆盘在下面）

3、将第n-1个从A移动到B

4、最后将n-2个从C移动到B（现在变为了大的在下面）

那么B到C也是一样的道理

#include
int move(char a, char c);
int hnt(int n,char a,char b,char c);
int main()
{
	int n;
	scanf("%d",&n);
	hnt(n,'a','b','c');
	return 0;
 } 
 
 int move(char a,char c)
 {
 	printf("%c->%c\n",a,c);
 }
 int hnt(int n,char a,char b,char c)
 {
 	if(n==1)
 	move(a,c);
 	else
 	{
 		hnt(n-1,a,c,b);//有n-1个圆盘从a经过c到b 
 		move(a,c);//第n个圆盘直接从a到c 
 		hnt(n-1,b,a,c);//有n-1个圆盘从b经过a到c 
	 }
 }