SLAM视觉里程计的理解

四种坐标系

SLAM中，用到四种坐标系：1、某点在现实世界坐标系中的坐标；2、点在相机坐标系中的坐标；3、归一化后的相机坐标（即Z=1，表示到相机距离为1的平面上的点的X、Y坐标）；4、像素二维坐标。

通过相机外参，即相机运动的旋转和平移，实现世界坐标系和相机坐标系的相互转化。通过相机内参，实现相机坐标系到像素坐标系的转化。相机内参在相机出厂后已经标定好，是已知量。SLAM求解的就是相机的外参，即相机的运动，以及点的世界坐标。

3D-3D：ICP

若RGB-D相机运动过程中拍下两张照片，根据相机内参，得到相机坐标系中的3D坐标（普通RGB相机内参转化后得到归一化的相机坐标，RGB-D相机根据深度，得到3D坐标）。这种问题称为3D-3D位姿估计问题，可以使用ICP（Iterative Closest Point）求解。求解ICP的非线性优化方法：

式中，为第一张图片中的点坐标，经过由李代数表示的相机旋转平移变换，理论上，应该与第二张图片中的点坐标重合，因此，使目标函数最小，求解最优李代数。

Gauss-Newton

这个非线性最优化问题，可以通过高斯牛顿法（Gauss-Newton）求解，思路如下：

对于最优化问题:

，自变量n维，目标函数m维，高斯牛顿法将其转化为：

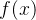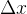是（注意不是）的雅可比矩阵 m行n列。通过求解，迭代求解最优解。

误差对李代数的导

回归到ICP的非线性优化方法，对李代数的导：（ps：就是变换矩阵T）

式中，R和t的取值：因为李代数是迭代求解，所以R和t就是当前迭代步的李代数对应的R和t。

ICP问题的雅可比矩阵就是，按照Gauss-Newton进行迭代求解，得到最优李代数。

3D-2D：PnP

有些时候，RGB-D相机不能有效得到深度，因此，不能得到3D坐标，只能得到2D坐标，即：第一张图片有深度，相机运动后拍摄的第二张图片没有深度，这种情况下，可以用PnP（Perspective-n-Point）方法求解。原理与ICP相似，区别在于：误差对李代数求导时，多了一步相机坐标系中空间坐标到像素坐标的链式法则，如下

 雅可比矩阵有所不同。

2D-2D

即两张照片都没有深度信息，这种情况用经典的八点法求解本质矩阵，由本质矩阵得到R和t。这个方法就不涉及李代数了。