239. 滑动窗口最大值(Hard)-双端队列之单调队列

239. 滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2：

输入：nums = [1], k = 1
输出：[1]

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104
• 1 <= k <= nums.length

题目解析

滑动窗口最大值，是用队列解决的经典问题，难度困难。

单调队列

在开始之前我先介绍一个之前没有讲过的队列，叫双端队列。

普通队列是限制仅在队尾进行插入，在队头进行删除操作的线性表，队列的插入叫做入队列，队列的删除叫做出队列。

而双端队列则是放开了这个限制，在队头和队尾两端都可以进行入队和出队操作的队列。

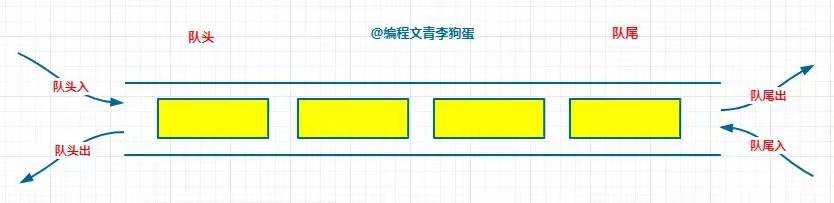
这么细看，其实对于队头或者队尾端，相当于是一个栈，后进的先出。

双端队列看上去这么的像栈和队列的结合体。

而有些时候，双端队列中还有受限的双端队列：一个是输出受限的双端队列，另一个是输入受限的双端队列。

输出受限的双端队列是：允许在一端进行入队和出队，但在另一端只允许入队的双端队列。

输入受限的双端队列是：允许在一段进行入队和出队，但在另一端只允许出队的双端队列。

输出受限的双端队列里，有一种情况，那就是队列里的各元素之间的关系具有单调性，这叫单调队列。

单调队列，顾名思义，所有队列里的元素都是按递增（递减）的顺序队列，这个队列的头是最小（最大）的元素。

题解

首先窗口向右滑动的过程就是将窗口最左侧的元素删除，同时在窗口的最右侧添加一个新的元素，这就要用到双端队列，然后找双端队列中的最大元素。

那剩下就是如何找到滑动窗口中的最大值。

那我们就可以只在队列中保留可能成为窗口最大元素的元素，去掉不可能成为窗口中最大元素的元素。

想象一下，如果要进来的是个值大的元素，那一定会比之前早进去的值小的元素晚离开队列，而且值大的元素在，都没值小的元素啥事，所以值小的元素直接弹出队列即可。

这样队列里其实维护的一个单调递减的单调队列。

图解

注：因为代码模拟方便，单调队列里存的是数组下标，在这为了演示的更加直观，图解中单调队列中用的是元素值。

假设 nums = [1, 3, -1, -3, 5, 3, 6, 7]，k = 3。

首先初始化一个单调队列和结果数组。

# 如果数组为空或 k = 0，直接返回空
if not nums or not k:
    return []
# 如果数组只有1个元素，直接返回该元素
if len(nums) == 1:
    return [nums[0]]
 
# 初始化队列和结果，队列存储数组的下标
queue = []
res = []

 第 1 步，数值为 1，此时单调队列为空，直接入队列。

第 2 步，数值为 3，queue 中有一个元素 1，3 > 1，所以按照我们之前说的，3 如果进入队列，那最大值只能会是 3，没有 1 的出头之日，所以 1 直接出队列即可。

# 对于新进入的元素，如果队列前面的数比它小，那么前面的都出队列
while queue and nums[queue[-1]] < nums[i]:
    queue.pop()
# 新元素入队列
queue.append(i)
 

第 3 步，数值为 -1，-1 < 3，所以 -1 直接入队列。

此时走过了 k = 3 个元素，当前的最大值就是单调队列最左侧的值，也就是 3。

# 当前的大值加入到结果数组中
if i >= k-1:
    res.append(nums[queue[0]])

第 4 步，窗口右移，此时对应下标数值为 -3，-3 < -1，所以 -3 直接入队列。

此时最大值依然还是 3。

第 5 步，窗口右移，下标 1 对应的数值 3 不在窗口内，但是 3 在 queue 内，所以 3 出队列。

# 如果当前队列最左侧存储的下标等于 i-k 的值，代表目前队列已满。
# 但是新元素需要进来，所以列表最左侧的下标出队列
if queue and queue[0] == i - k:
    queue.pop(0)

 此时下标对应的数值为 5，5 分别大于 -1 和 -3，所以 -1 和 -3 出队列，5 入队列，此时的最大值为 5。

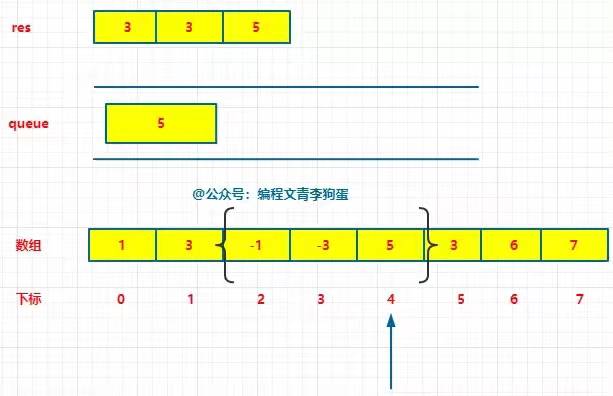
第 6 步，窗口右移，当前下标对应的数值为 3，3 < 5，所以 3 直接入队列，此时的最大值是 5。

第 7 步，窗口右移，当前下标对应的数值为 6，6 大于 queue 中的 5 和 3，所以 queue 中的 5 和 3 出队列，然后 6 入队列，此时最大的值为 6。

第 8 步，窗口右移，当前下标对应的数值为 7，7 > 6，所以 queue 中 6 出队列，7 入队列，当前最大值为 7。

此时数组扫描完，直接输出 res 的结果即可。

本题的解法，数组被从头到尾扫描一遍，每个元素的下标最多进出队列一次，所以时间复杂度为 O(n)。

因为创建了一个额外的大小为 k 的队列存储，所以本题空间复杂度为 O(k)。

代码实现：

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
 
        # while(right < len(nums)):
        #     res.append(max(nums[left:left+k]))
        #     left += 1
        #     # window.append(nums[right])
        #     right += 1
 
         # 如果数组为空或 k = 0，直接返回空
        if not nums or not k:
            return []
        # 如果数组只有1个元素，直接返回该元素
        if len(nums) == 1:
            return [nums[0]]
 
        window, res = [], []# window存储数组的下标，res存储最大值结果
        for i in range(len(nums)):
            # 如果当前队列最左侧存储的下标等于 i-k 的值，代表目前队列已满。
            # 但是新元素需要进来，所以列表最左侧的下标出队列
            if(window and window[0] == i-k):
                window.pop(0)
            # 对于新进入的元素，如果队列前面的数比它小，那么前面的都出队列(单调递减队列实现)
            while(window and nums[window[-1]] < nums[i]):#window[-1]表示队尾的最后一个元素
                window.pop()#队尾最后一个元素出队（因为要保证队首元素为最大值，所以只能从右边出队）
            # 新元素下标入队列，窗口右移动
            window.append(i)
            # 当前的大值加入到结果数组中
            if(i >= k-1):
                res.append(nums[window[0]])
        return res     
 
        

 参考：ACM 选手图解 LeetCode 滑动窗口最大值 | 编程文青李狗蛋