22级第三次比赛题解

A (1). Ashy与几何(贪心+几何)

求最小移动次数，我们的思路肯定是贪心的去移动，每次销都放在起点与终点的连线上，这样保证了要移动的距离最短，那如果起点与中点的距离不是我们移动距离的倍数，那么我们需要额外花费一次移动次数

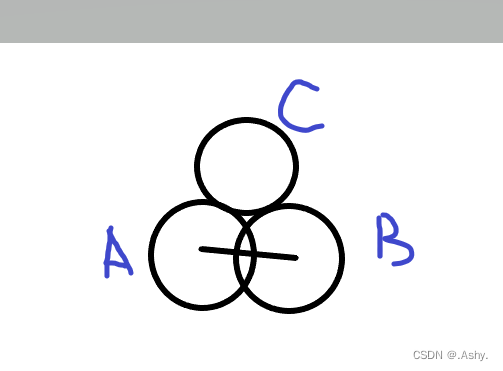
就像这样 ， 我们要从 A - B , 但是A - B 圆心之间的距离不够 2r ， 我们借助一下C ， 先把A转移到C，在转移到B即可。

那么最后的答案就是 ceil(dis(a,b) /(2 * r))

double r , a , b , c , d;

int main(){

	cout << fixed ;
	cin >> r >>  a >> b >> c >> d;
	double x1 = abs(a - c);
	double x2 = abs(b - d);
	double sumx = sqrt(x1 * x1 + x2 * x2);
	int ans = ceil(sumx / (2 * r));
	cout << ans;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

B (2). One eye question of hengheng(前缀和)

可以暴力做 ， 但是这是个前缀和算法的裸题，在这里给出前缀和算法，前缀和算法可以把时间复杂度优化到O(n)

int n , q , a[N] , sum[N];

int main(){

	cin >> n;
	for(int i=1;i<=n;i++){
		cin >> a[i];
		sum[i] = sum[i-1] + a[i];
	} 
	int l , r;
	cin >> q;
	while(q--){
		cin >> l >> r;
		cout << sum[r] - sum[l-1] << "\n" ;
	}

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

C Fox hate oranges(模拟)

这个题出的很怪，怪就怪在讨厌句子的人手里会有橘子，但是这不妨碍我们做题
模拟一下即可，要注意的就是当我手里没有橘子的时候，我去讨厌橘子的人哪里是不会战斗的，这是个大坑点

int n , m , k;
int a[101];
bool vis[101];

int main(){
	cin >> n >> m >> k;
	
	for(int i=1;i<=m;i++) cin >> a[i];
	for(int i=1;i<=k;i++){
		int id;cin >> id;
		vis[id] = 1;//标记讨厌橘子的人
	}
	
	for(int i=1;i<=m;i++){
		if(!vis[i]){//这个人喜欢橘子
			if(n > a[i]) n -= a[i]; //橘子够 ， 给他橘子
			else{
				a[i] = n;
				n = 0;//橘子不够 ， 全给他
			}
		}else{//讨厌橘子
			if(n == 0) continue; //我没有橘子，不战斗
			else if(n >= a[i]){//我有橘子，战斗我赢
				a[i] += n / 2;
				n -= n / 2;
			}else{//我有橘子，战斗我输
				n += a[i] / 2;
				a[i] -= a[i] / 2;
			}
		}
	}
	
	cout << n << "\n" ;
	for(int i=1;i<=m;i++) cout << a[i] << " " ;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

D KingZhang’s Similar pair (思维)

要满足条件首先数字的个数一定要是偶数个，这是毋庸置疑的，这样的话，情况就很好讨论了

1. 奇数和偶数都是偶数个

这样必然能分组成功

2. 奇数和偶数都是奇数个

这样的话，找一个奇数和一个偶数满足差为 1即可
我的查找方法是先排序找相邻数的差，怎么找都行

int n , k;
int a[N] , cnt1 , cnt2;

int main(){

	cin >> n;
	
	if(n % 2 != 0){
		cout << "NO\n";
		return 0;
	}
	
	for(int i=1;i<=n;i++){
		cin >> a[i];
		if(a[i] % 2) cnt1++;
		else cnt2++;
	}
	
	sort(a+1,a+1+n);
	
	if(cnt1 % 2 == 0){//都是偶数个
		cout << "YES" ;
	}else{//否则找有没有差是1的
		bool f= 0;
		for(int i=1;i<n;i++){
			if(a[i+1] - a[i] == 1){
				f = 1;break;
			}
		}
		
		if(f){
			cout << "YES";
		}else{
			cout << "NO";
		}	
	}
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

E (5). 38秒你敢交我A题？

水题 ， 记下数就行

int n , t , a[N];

int main(){

	cin >> n;
	for(int i=1;i<=n;i++) cin >> a[i];
	sort(a+1,a+1+n);
	int k = a[n/2+1];
	int cnt = 0;
	for(int i=1;i<=n;i++){
		if(a[i] == k) cnt++;
	}
	if(cnt == 1){
		cout << "Fox%xoF " << k;
	}else{
		cout << "Bad%daB" ;
	}

	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

F (6). How many numbers are there

水题 ， 搞一个桶，存进去遍历一下就可

int n , t , a[N] , id;

int main(){

	cin >> n;
	
	for(int i=1;i<=n;i++){
		cin >> id;a[id] = 1;
	}
	
	int cnt = 0;
	for(int i=1;i<=100000;i++){
		if(a[i] == 1) cnt++;
	}
	cout << cnt;

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

G (7). Jump lattice (思维)

要找最小的D，只要每次跳都是在 1 的左边一个 2的位置跳，那么答案就是最长的连续 1 的个数 + 1

int n , k;
int a[N],cnt = 1 , max1 = -inf;

int main(){

	cin >> n;
	
	for(int i=1;i<=n;i++){
		cin >> k;
		if(k == 2){
			max1 = max(cnt , max1);
			cnt = 1;
		}else{
			cnt++;
		}
	}
	
	max1 = max(cnt  , max1);
	
	cout << max1 ;

	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

H (8). CCoolGuang Conjecture(数论)

这是2020CCPC威海站D题数据弱化版，防AK的，有够难，难为验题的我了

首先看 rad 的定义 ， rad( c ) 是 c的质因子乘积
首先我们可以发现性质1

1. 根据唯一分解定理，每一个数都可以分解为质因子的乘积
   如果一个数的质因子分解后幂次都是 1 ， 那么满足 rad( c ) == c
   但是如果分解后出现幂次大于 1 的数，那肯定满足 rad( c ) < c
   所以我们把 c 质因子分解后 ， 如果幂次都是 1,那么rad( abc ) >= c , 不可能出现 rad( abc ) < c

然后就是一个数质因子分解后如果有一个质因子幂次大于 1 ， 这样必然存在 a , b 满足rad( abc ) < c且 a + b == c , 为什么呢 ， 我们来证明一下

假如 c == 75 ， 分解后就是 5 * 5 * 3
我们必然能拆掉那个出现多次的质数 5 * 5 * 3 -> (1 + 4) * 5 * 3
a = 1 * 5 * 3
b = 4 * 5 * 3
那么 a * b * c 的质因数就是 2 5 3 必然小于 5 * 5 * 3

我举这个例子的意思就是 ， 一个重复的质因子拆分相乘后，生成的新的质因子一定小于拆分的质因子，因此得证。

对所给数质因子分解 ， 分解后幂次都是 1 的数满足条件

int p[N] , cnt , t , n;

bool isp(int n){
	if(n < 2) return 0;
	for(int i=2;i*i<=n;i++)
		if(n % i == 0) return 0;
	return 1;
}

int main(){
	
	for(int i=1;i<=100;i++) if(isp(i)) p[++cnt] = i;
	
	cin >> t;
	
	while(t--){
		cin >> n;
		
		bool f = 0;
		
		for(int i=1;i<=cnt;i++){
			int cnt = 0;
			while(n % p[i] == 0){
				cnt++;
				n /= p[i];
			}
			if(cnt > 1){
				f = 1;break;
			}
		}
		
		if(f) cout << "yes\n";
		else cout << "no\n";
	}
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

I (9). Cutele想去打篮球(排序 ， 思维)

我们给所有的数排个序 ， 可以发现我么要找的这两个数一定是相邻的数，非相邻的数间距一定会大于相邻的数，而且相邻的数恰好可以满足题目中的条件，所以题目就变成了找相邻数的最小值问题

int n , t , a[N] , id;

int min1 = inf;

int main(){

	cin >> n;
	
	for(int i=1;i<=n;i++) cin >> a[i];
	
	sort(a+1,a+1+n);
	
	for(int i=1;i<n;i++){
		min1 = min(min1 , abs(a[i] - a[i+1]));
	}
	
	cout << min1 ;
	
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

J (10). The most difficult question

const int inf = 1e9 + 10;
int n , t , a[N] , id;

ll ans = 1;

int main(){

	cin >> n;
	
	for(int i=1;i<=n;i++) ans = ans * i % p;
	
	cout << ans; 
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

K (11). 异世相遇

注意用星尘抽卡后还会获得星辰

int n , t , a[N] , m;
int ans = 0;
int main(){

	cin >> n >> m;
	
	while(n >= 160 || m >= 75){
		int k1 = n / 160; //原石抽卡次数
		ans += k1;
		n -= k1 * 160; //剩余原石数量
		m += k1 * 15;//星辰数量
		int k2 = m / 75; //星辰抽卡次数
		ans += k2;
		m -= k2 * 75;
		m += k2 * 15;//剩余星辰数量
	}
	
	cout << ans;
	
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

L (12). 绘制图像

主对角线是 i == j . 副对角线是 $i+j==n+1$

int n;
char c[100][100];
char a , b , s;

int main(){

	cin >> n >> a >> b >> s;
	
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i == 1 || i == n) c[i][j] = a;
			else if(j == 1 || j == n) c[i][j] = b;
			else if(i == j || i + j == n + 1) c[i][j] = s;
			else c[i][j] = ' ';
			cout << c[i][j];
		}
		cout << "\n" ;
	}

	
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

M (13). UpMing的CrossFire幻境

先全换成小写 ， 然后搜索一下就行

int n;
string s;
int a[N],cnt;

int main(){

	cin >> n >> s;
	
	int len = s.size();

	for(int i=0;i<len;i++) s[i] = tolower(s[i]);
	
	for(int i=0;i<len-2;i++){
		if(s[i] == 'a' && s[i+1] == 'c' && s[i+2] == 'm'){
			a[++cnt] = i;
		}
	}
	cout << cnt << "\n" ;
	for(int i=cnt;i>=1;i--) cout << a[i] << "  "[i != 1];
	

	
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25