树链剖分与线段树

一 说明

在树中进行点更新、区间更新、区间查询等操作，可以使用线段树来维护和处理。

二 图解

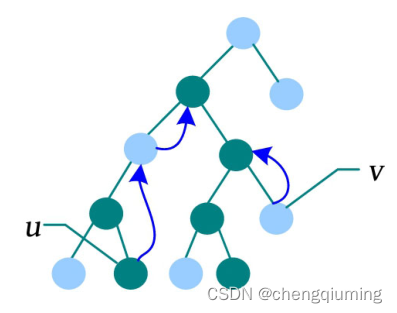
一棵树如下图所示。

树链剖分之后的节点序列和下标序列如下图所示。

节点序列对应的权值如下图所示。

根据 w[] 序列创建线段树，如下图所示。

查询节点 u 到 v 路径上节点权值的最值与和值的方法如下。

• 若 u 和 v 在同一条重链上，则在线段树上查询其对应的下标区间 [id[u ],id[v ]]即可。

• 若 u 和 v 不在同一条重链上，则一边查询，一边将 u 和 v 向同一条重链上移。对于顶端节点深度大的节点，先查询其到顶端节点的区间，然后一边上移一边查询，直到上移到同一条重链上，再查询在同一条重链上的区间。

查询节点 6～9 权值的最值与和值（包括6和9节点），过程如下。

1 读取 top[6]=1，top[9]=2，两者不相等则说明其不在一条重链上，且 top[9]的深度大，先查询 top[9]～9之间的最值与和值。

首先得到节点 2 和 9 对应的节点序列下标 7 和 9。

然后在线段树中查询 [7, 9] 区间的最值与和值。[7,9] 区间的最值与和值：Max=15，Sum=22。

2 将 u 上移到 top[9]（2号节点）的父节点，即 1 号节点，此时 1 和 6 在同一条链上。

节点 1 和 6 对应的线段树下标为 1 和 3。

在线段树中查询到 [1, 3] 区间的最值与和值分别为 20、31，如下图所示 。 再与前面的结果求最大值与和值 ， 则 Max=max(Max,20)=max(15, 20)=20，Sum=Sum+31=22+31=53。

区间更新的方法与此类似，若不在一条链上，则一边更新，一边向同一条链上靠，最后在同一条链上更新即可。

注意：更新和查询时均需要先得到节点对应的线段树下标，再在线段树上更新和查询。